题目内容
椭圆上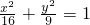 一点P到直线x+y+10=0的距离最小值为
一点P到直线x+y+10=0的距离最小值为
- A.

- B.3

- C.

- D.
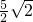
D
分析:设与直线x+y+10=0平行的直线方程为:x+y+c=0,与椭圆方程联立,消元,令△=0,可得c的值,求出两条平行线间的距离,即可求得椭圆上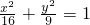 一点P到直线x+y+10=0的距离最小值.
一点P到直线x+y+10=0的距离最小值.
解答:设与直线x+y+10=0平行的直线方程为:x+y+c=0,与椭圆方程联立,消元可得25x2+32cx+16c2-144=0
令△=1024c2-100(16c2-144)=0,可得c=±15
∴两条平行线间的距离为 =
=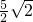 或
或
∴椭圆上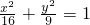 一点P到直线x+y+10=0的距离最小值为
一点P到直线x+y+10=0的距离最小值为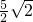
故选D.
点评:本题考查直线与椭圆的位置关系,解题的关键是求出与直线x+y+10=0平行,且与椭圆相切的直线方程.
分析:设与直线x+y+10=0平行的直线方程为:x+y+c=0,与椭圆方程联立,消元,令△=0,可得c的值,求出两条平行线间的距离,即可求得椭圆上
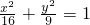 一点P到直线x+y+10=0的距离最小值.
一点P到直线x+y+10=0的距离最小值.解答:设与直线x+y+10=0平行的直线方程为:x+y+c=0,与椭圆方程联立,消元可得25x2+32cx+16c2-144=0
令△=1024c2-100(16c2-144)=0,可得c=±15
∴两条平行线间的距离为
 =
=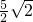 或
或
∴椭圆上
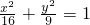 一点P到直线x+y+10=0的距离最小值为
一点P到直线x+y+10=0的距离最小值为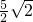
故选D.
点评:本题考查直线与椭圆的位置关系,解题的关键是求出与直线x+y+10=0平行,且与椭圆相切的直线方程.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 一点P到直线x+y+10=0的距离最小值为( )
一点P到直线x+y+10=0的距离最小值为( ) B、3
B、3 C、
C、 D、
D、 
 一点P到直线x+y+10=0的距离最小值为( )
一点P到直线x+y+10=0的距离最小值为( )


