题目内容
 如图ABCD-A1B1C1D1为正方体,一只青蛙开始在顶点A处,它每次可随意跳到相邻三顶点之一,若在五次内跳到C1点,则停止跳动;若5次内不能跳到C1点,跳完五次也停止跳动,求:
如图ABCD-A1B1C1D1为正方体,一只青蛙开始在顶点A处,它每次可随意跳到相邻三顶点之一,若在五次内跳到C1点,则停止跳动;若5次内不能跳到C1点,跳完五次也停止跳动,求:
(1)5次以内能到C1点的跳法有多少种?
(2)从开始到停止,可能出现的跳法有多少种?
解:(1)由题意知本题是一个分步计数问题,如果不回跳,那么跳三次可到达C1点,
第一跳有3种;第二跳有2种;第三跳有1种,
根据乘法原理知共有N1=3×2×1=6种.
(2)由题意知本题是一个分类计数问题,
由条件青蛙的跳法只可能出现两种情况,
其一跳三次到达C1点,有6种跳法,
其二跳五次停止(前三次不到C1点),有(33-6)•32=189,
故共有6+189=195种不同的跳法.
分析:(1)由题意知本题是一个分步计数问题,如果不回跳,那么跳三次可到达C1点,第一跳有3种;第二跳有2种;第三跳有1种,相乘得到结果.
(2)本题是一个分类计数问题,由条件青蛙的跳法只可能出现两种情况,其一跳三次到达C1点,有6种跳法,其二跳五次停止(前三次不到C1点),根据分类计数得到结果.
点评:本题考查加法原理和乘法原理,同时也考查了学生分析解答问题的能力,本题解题的关键是从已知分析得到,青蛙不能经过跳1次、2次或4次到达,应从青蛙跳3次到达和青蛙一共跳5次后停止两种情况入手分析计算,本题是一个中档题目.
第一跳有3种;第二跳有2种;第三跳有1种,
根据乘法原理知共有N1=3×2×1=6种.
(2)由题意知本题是一个分类计数问题,
由条件青蛙的跳法只可能出现两种情况,
其一跳三次到达C1点,有6种跳法,
其二跳五次停止(前三次不到C1点),有(33-6)•32=189,
故共有6+189=195种不同的跳法.
分析:(1)由题意知本题是一个分步计数问题,如果不回跳,那么跳三次可到达C1点,第一跳有3种;第二跳有2种;第三跳有1种,相乘得到结果.
(2)本题是一个分类计数问题,由条件青蛙的跳法只可能出现两种情况,其一跳三次到达C1点,有6种跳法,其二跳五次停止(前三次不到C1点),根据分类计数得到结果.
点评:本题考查加法原理和乘法原理,同时也考查了学生分析解答问题的能力,本题解题的关键是从已知分析得到,青蛙不能经过跳1次、2次或4次到达,应从青蛙跳3次到达和青蛙一共跳5次后停止两种情况入手分析计算,本题是一个中档题目.

练习册系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
如图,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
| ||
| 3 |
| A、相交 | B、平行 |
| C、垂直 | D、不能确定 |
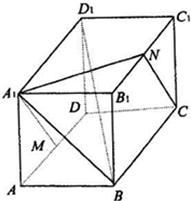 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=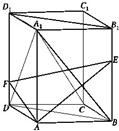 如图,在长方体ABCD-A1B1C1D1中,点E、F分别BB1、DD1上,且AE⊥A1B,AF⊥A1D.
如图,在长方体ABCD-A1B1C1D1中,点E、F分别BB1、DD1上,且AE⊥A1B,AF⊥A1D.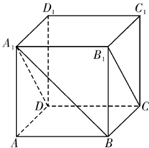 如图,在正方体ABCD-A1B1C1D1中,直线A1B与平面A1B1CD所成的角的大小等于
如图,在正方体ABCD-A1B1C1D1中,直线A1B与平面A1B1CD所成的角的大小等于 (2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.
(2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.