题目内容
3. 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.(1)求三棱锥E-PAD的体积;
(2)证明:无论点E在边BC的何处,都有AF⊥PE.
分析 (1)转换底面,代入体积公式计算;
(2)利用线线垂直证明AF⊥平面PBC,即可得出结论.
解答 (1)解:∵PA⊥平面ABCD,且四边形ABCD为矩形.
∴${S_{△EAD}}=\frac{1}{2}AD•AB=1$,…(3分)
∴${V_{E-PAD}}={V_{P-EAD}}=\frac{1}{3}{S_{EAD}}•PA=\frac{1}{3}$…(6分)
(2)证明:∵PA⊥平面ABCD,∴PA⊥AB,
又∵PA=AB=1,且点F是PB的中点,
∴AF⊥PB…(8分)
又PA⊥BC,BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,
又AF?平面PAB,∴BC⊥AF…(10分)
由$\left\{{\begin{array}{l}{AF⊥PB}\\{AF⊥BC}\\{PB∩BC=B}\end{array}⇒}\right.$AF⊥平面PBC,又∵PE?平面PBC
∴无论点E在边BC的何处,都有AF⊥PE成立.…(12分)
点评 本题给出特殊的四棱锥,考查了线面垂直的证明与性质的运用,考查了学生的空间想象能力与推理论证能力,关键是要熟练掌握定理的条件.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
14.函数f(x)=cos2x+$\sqrt{3}$sinxcosx,
命题p:?x0∈R,f(x0)=-1,
命题q:?x∈R,f(2π+x)=f(x),
则下列命题中为假命题的是( )
命题p:?x0∈R,f(x0)=-1,
命题q:?x∈R,f(2π+x)=f(x),
则下列命题中为假命题的是( )
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | ¬p∨¬q |
11.已知i为虚数单位,复数z=-$\frac{1}{3}$+$\frac{2\sqrt{2}}{3}$i的共轭复数为$\overline{z}$,则$\overline{z}$的虚部为( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$i | D. | -$\frac{2\sqrt{2}}{3}$i |
18.若函数f(x)的导函数f′(x)的图象如图所示.则( )
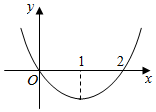

| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |
8.等差数列{an}的各项均为正值,若a3+2a6=6,则a4a6的最大值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
15.定义集合A={x|2x≥1}},B={x|${{{log}_{\frac{1}{2}}}$x<0},则A∩∁RB=( )
| A. | (1,+∞) | B. | [0,1] | C. | [0,1) | D. | [0,2) |