题目内容
(理) 设O为坐标原点,向量| OA |
| OB |
| OP |
| QA |
| QB |
分析:由已知中O为坐标原点,向量
=(1,2,3),
=(2,1,2),
=(1,1,2),点Q在直线OP上运动,我们可以设
=λ
=(λ,λ,2λ),求出向量
,
的坐标,代入空间向量的数量积运算公式,再根据二次函数的性质,可得到满足条件的λ的值,进而得到点Q的坐标.
| OA |
| OB |
| OP |
| OQ |
| OP |
| QA |
| QB |
解答:解:∵
=(1,1,2),点Q在直线OP上运动,
设
=λ
=(λ,λ,2λ)
又∵向量
=(1,2,3),
=(2,1,2),
∴
=(1-λ,2-λ,3-2λ),
=(2-λ,1-λ,2-2λ)
则
•
=(1-λ)×(2-λ)+(2-λ)×(1-λ)+(3-2λ)×(2-2λ)=6λ2-16λ+10
易得当λ=
时,
•
取得最小值.
此时Q的坐标为(
,
,
)
故答案为:(
,
,
)
| OP |
设
| OQ |
| OP |
又∵向量
| OA |
| OB |
∴
| QA |
| QB |
则
| QA |
| QB |
易得当λ=
| 4 |
| 3 |
| QA |
| QB |
此时Q的坐标为(
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
故答案为:(
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
点评:本题考查的知识点是空间向量的数量积运算,其中根据空间向量数量积的坐标运算公式,求出
•
的表达式,进而将问题转化为一个二次函数最值问题,是解答本题的关键.
| QA |
| QB |

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
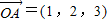 ,
,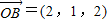 ,
,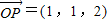 ,点Q在直线OP上运动,则当
,点Q在直线OP上运动,则当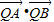 取得最小值时,点Q的坐标为 .
取得最小值时,点Q的坐标为 .