题目内容

已知G点是△ABC的重心，过G点作直线与AB、AC两边分别交于M、N两点，设
AM
=x
AB
，
AN
=y
AC
，则
1
x
+
1
y
=
3
3
．
分析：由G为三角形的重心，可得
AG
=
1
3
（
AB
+
AC
），结合
AM
=x
AB
，
AN
=y
AC
，根据M，G，N三点共线，易得到x，y的关系式，整理后即可得到答案．
解答：解：∵G为三角形的重心，
∴
AG
=
1
3
（
AB
+
AC
），
∴
MG
=
AG
-
AM
=
1
3
（
AB
+
AC
）-x
AB
=（
1
3
-x）
AB
+
1
3
AC
，
GN
=
AN
-
AG
=y
AC
-
1
3
（
AB
+
AC
）=-
1
3
AB
+（y-
1
3
）
AC
，
∵
MG
与
GN
共线，
∴存在实数λ，使得
MG
=λ
GN
，
即（
1
3
-x）
AB
+
1
3
AC
=λ[-
1
3
AB
+（y-
1
3
）
AC
]，
由向量相等的定义可得
1
3
-x=-
1
3
λ
1
3
=λ(y-
1
3
)
，
消去λ可得x+y-3xy=0，
两边同除以xy整理得
1
x
+
1
y
=3
故答案为：3
点评：本题考查的知识点是向量的线性运算性质及几何意义，向量的共线定理，及三角形的重心，属中档题．
练习册系列答案
相关题目
已知点G是△ABC的重心，A（0，-1），B（0，1）．在x轴上有一点M，满足|
MA
|=|
MC
|，
GM
=λ
AB
(λ∈R)（若△ABC的顶点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则该三角形的重心坐标为G(
x1+x2+x3
3
，
y1+y2+y3
3
)）．
（1）求点C的轨迹E的方程．
（2）设（1）中曲线E的左、右焦点分别为F1、F2，过点F2的直线l交曲线E于P、Q两点，求△F1PQ面积的最大值，并求出取最大值时直线l的方程．
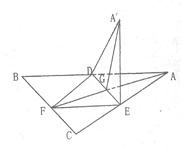精英家教网如图，正△ABC的中线AF与中位线DE相交于点G，已知△A′DE是△AED绕边DE旋转过程中的一个图形．
（I）求证点A′在平面ABC上的射影在线段AF上；
（II）求当A′E⊥BD时△A′DE所转过的角的大小．
如图，正△ABC的中线AF与中位线DE相交于G，已知△A'ED是△AED绕DE旋转过程中的一个图形，现给出下列四个命题：
①动点A'在平面ABC上的射影在线段AF上；
②恒有平面A'GF⊥平面BCED；
③三棱锥A'-FED的体积有最大值；
④面直线A'E与BD不可能垂直．
其中正确的命题的序号是
①②③
①②③
．
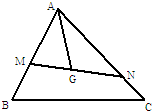精英家教网如图所示，已知点G是△ABC的重心，过G作直线与AB、AC两边分别交于M、N两点，且
AM
=x
AB
，
AN
=y
AC
，则
xy
x+y
的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网