题目内容
1.设等差数列{an}的前n项和为Sn,满足a2=4,S5=30.(1)求数列{an}的通项公式an;
(2)令bn=an2n-1,求数列{an}的前n项和Tn.
分析 (1)设等差数列{an}的公差为d,由等差数列的通项公式、等比中项的性质列出方程组,求出a1和d,代入等差数列的通项公式求出an;
(2)由(1)和指数的运算性质化简bn,利用错位相减法和等比数列的前n项和公式求出前n项和Tn.
解答 解:(1)设等差数列{an}的公差为d,
由题意得$\left\{\begin{array}{l}{{a}_{1}+d=4}\\{5{a}_{1}+\frac{5×4}{2}×d=30}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=2}\end{array}\right.$,
所以an=2+(n-1)•2=2n;
(2)由(1)得,bn=an2n-1=n•2n,
所以Tn=1•21+2•22+3•23+…+n•2n,①
2Tn=1•22+2•23+3•24+…+n•2n+1,②
①-②得,-Tn=21+22+23+…+2n-n•2n+1
=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1=(1-n)2n+1-2,
所以Tn=(n-1)2n+1+2.
点评 本题考查等差数列的通项公式,等比中项的性质,等比数列的前n项和公式,以及错位相减法求数列的和,考查方程思想,化简、变形能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
11.掷三颗骰子(各面上分别标有数字1至6的质地均匀的正方体玩具),恰有一颗骰子掷出的点数可以被3整除的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{19}{27}$ |
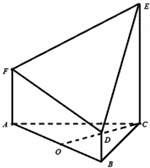 如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.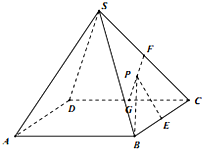 如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点. 已知在长方体ABCD-A1B1C1D1中,E、M、N分别是BC、AE、D1C的中点,AD=AA1,AB=2AD
已知在长方体ABCD-A1B1C1D1中,E、M、N分别是BC、AE、D1C的中点,AD=AA1,AB=2AD 如图所示,在棱长为a的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,若此最小值为$2\sqrt{2+\sqrt{2}}$,则a的值是( )
如图所示,在棱长为a的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,若此最小值为$2\sqrt{2+\sqrt{2}}$,则a的值是( )