题目内容
8.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(x,y).则“x=-2且y=-4”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”的( )| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据向量平行的性质及判定得到y=2x,进而判断“y=2x”和“x=-2,y=-4”的关系即可.
解答 解:若“$\overrightarrow{a}$∥$\overrightarrow{b}$”,则满足y=2x,
由x=-2,y=-4能推出y=2x,是充分条件,
由y=2x推不出x=-2,y=-4,不是必要条件,
故选:B.
点评 本题考查了充分必要条件,考查了平行向量问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.等差数列{an}中,a${\;}_{m}=\frac{1}{k}$,ak=$\frac{1}{m}$(m≠k),则该数列前mk项之和为( )
| A. | $\frac{mk}{2}-1$ | B. | $\frac{mk}{2}$ | C. | $\frac{mk+1}{2}$ | D. | $\frac{mk}{2}+1$ |
16.条件p:x2-4x-5<0是条件q:x2+6x+5>0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 非充分又非必要条件 |
3.已知函数f(x)=loga(2x+b-1)的部分图象如图所示,则a,b所满足的关系是( )


| A. | 0<b-1<a<1 | B. | 0<a-1<b<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b-1<1 |
20.△ABC的内角A,B,C的对边分别是a,b,c,若B=2A,a=1,b=$\sqrt{3}$,则边c=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2或1 |
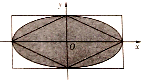 如图,已知矩形长为6,宽为4,在矩形内随机地撒75颗黄豆,数得落在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外的黄豆数16颗,现随机向椭圆内丢一粒豆子,则豆子落在菱形(菱形顶点为椭圆的顶点)区域内的概率为$\frac{75}{118}$.
如图,已知矩形长为6,宽为4,在矩形内随机地撒75颗黄豆,数得落在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外的黄豆数16颗,现随机向椭圆内丢一粒豆子,则豆子落在菱形(菱形顶点为椭圆的顶点)区域内的概率为$\frac{75}{118}$. 为奇函数,则
为奇函数,则 ______.
______.