题目内容
函数f（x）=sin2x在区间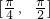
上的最大值是
- A.1
- B.
- C.
- D.1+
A
分析：先利用二倍角公式对原函数进行整理，再借助于余弦函数的单调性即可求解．
解答：∵f（x）=sin2x=
，
≤x≤
?≤2x≤π，
而y=cosx在[，π]上递减，
∴当2x=π即x=时，函数f（x）=sin2x有最大值，此时f（x）=
=1
故选A．
点评：本题主要考查二倍角的余弦公式的应用．二倍角的余弦公式：cos2x=cos2x-sin2x=2cos2x-1=1-2sin2x．
分析：先利用二倍角公式对原函数进行整理，再借助于余弦函数的单调性即可求解．
解答：∵f（x）=sin2x=
，≤x≤?≤2x≤π，而y=cosx在[
，π]上递减，∴当2x=π即x=
时，函数f（x）=sin2x有最大值，此时f（x）==1故选A．
点评：本题主要考查二倍角的余弦公式的应用．二倍角的余弦公式：cos2x=cos2x-sin2x=2cos2x-1=1-2sin2x．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则