题目内容
已知关于x的函数f(x)=ax2-4bx+1.
(1)若a=0,b∈(-1,2)求函数y=f(x)是增函数的概率;
(2)设点(a,b)是区域
内的随机点,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(1)若a=0,b∈(-1,2)求函数y=f(x)是增函数的概率;
(2)设点(a,b)是区域
|
分析:(1)根据a=0,f(x)=-4bx+1,是增函数,则-1<b<0,而试验发生所包含的区间为b∈(-1,2),利用几何概率的计算公式可求
(2)根据函数是增函数,得到试验发生包含的事件对应的区域和满足条件的事件对应的区域,做出面积,利用几何概型计算公式得到结果.
(2)根据函数是增函数,得到试验发生包含的事件对应的区域和满足条件的事件对应的区域,做出面积,利用几何概型计算公式得到结果.
解答:(本小题满分12分)
解:(1)当a=0,f(x)=-4bx+1,若y=f(x)是增函数,则b<0.…(2分)
∵b∈(-1,2),∴所求事件的概率为
.…(4分)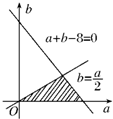
(2)∵函数f(x)=ax2-4bx+1的图象的对称轴为x=
,要使函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,当且仅当a>0且
≤1,即2b≤a.,…(6分)
依条件可知试验的全部结果所构成的区域为
构成所求事件的区域为如图阴影部分.…(8分)
由
得交点坐标为(
,
)..…(10分)
∴所求事件的概率为P=
=
..…(12分)
解:(1)当a=0,f(x)=-4bx+1,若y=f(x)是增函数,则b<0.…(2分)
∵b∈(-1,2),∴所求事件的概率为
| 1 |
| 3 |

(2)∵函数f(x)=ax2-4bx+1的图象的对称轴为x=
| 2b |
| a |
| 2b |
| a |
依条件可知试验的全部结果所构成的区域为
|
构成所求事件的区域为如图阴影部分.…(8分)
由
|
| 16 |
| 3 |
| 8 |
| 3 |
∴所求事件的概率为P=
| ||||
|
| 1 |
| 3 |
点评:本题主要考查了由长度、面积度量的几何概率的求解,几何概型的概率的值是通过长度、面积、和体积的比值得到.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目