题目内容
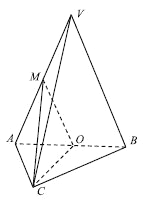
【题目】如图所示,在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,现沿
,现沿![]() 将
将![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
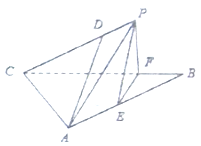
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)建立空间直角坐标系,结合直线的方向向量和平面的法向量即可证得![]() 平面
平面![]() ;
;
(2)求得平面的法向量,结合夹角公式可得二面角![]() 的余弦值是
的余弦值是![]() .
.
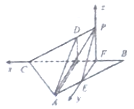
试题解析:
(1)因为![]() ,
, ![]() ,所以建立以点
,所以建立以点![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴的空间直角坐标系,如图所示.
轴的空间直角坐标系,如图所示.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
易知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
又因为![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)知![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即![]() .
.
令![]() ,解得
,解得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
又因为![]() 为平面
为平面![]() 的一个法向量,所以
的一个法向量,所以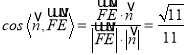 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某校计划面向高一年级1240名学生开设校本选修课程,为确保工作的顺利实施,按性别进行分层抽样,现抽取124名学生对社会科学类、自然科学类这两大类校本选修课程进行选课意向调查,其中男生有65人.在这124名学生中选修社会科学类的男生有22人、女生有40人.
(1)根据以上数据完成下列列联表;
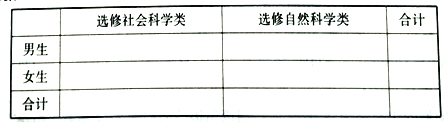
(2)判断能否有99.9%的把握认为科类的选修与性别有关?
附: 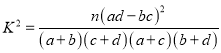 ,其中
,其中![]()
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |