题目内容
已知P:方程x2+mx+1=0有两个不等的负根;q:方程 4x2+4(m-2)x+1=0
无实根.若p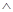 q为假,p
q为假,p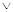 q为真,求m的取值范围.
q为真,求m的取值范围.
无实根.若p
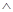 q为假,p
q为假,p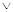 q为真,求m的取值范围.
q为真,求m的取值范围.
先把p、q为真时,m的取值范围求出来,然后根据p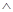 q为假,p
q为假,p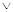 q为真,确定p、q一真一假,再分两种情况进行求解,最后求并集即可.
q为真,确定p、q一真一假,再分两种情况进行求解,最后求并集即可.
解:若方程x2+mx+1=0有两个不等的负根则 (3分)
(3分)
若4x2+4(m-2)x+1=0方程无实根则 ,解得1<m<3,即q:1<m<3(6分)
,解得1<m<3,即q:1<m<3(6分)
因为p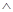 q为假,p
q为假,p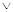 q为真,则p为真,q为假或者q为真,p为假(8分)
q为真,则p为真,q为假或者q为真,p为假(8分)
则 (12分)
(12分)
评注:少一种情况扣2分
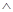 q为假,p
q为假,p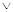 q为真,确定p、q一真一假,再分两种情况进行求解,最后求并集即可.
q为真,确定p、q一真一假,再分两种情况进行求解,最后求并集即可.解:若方程x2+mx+1=0有两个不等的负根则
 (3分)
(3分)若4x2+4(m-2)x+1=0方程无实根则
 ,解得1<m<3,即q:1<m<3(6分)
,解得1<m<3,即q:1<m<3(6分)因为p
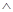 q为假,p
q为假,p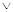 q为真,则p为真,q为假或者q为真,p为假(8分)
q为真,则p为真,q为假或者q为真,p为假(8分)则
 (12分)
(12分)评注:少一种情况扣2分

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 :
: ,其中
,其中 ,命题
,命题 :
: ,
, ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围; 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.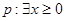 ,
,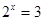 ,则( )
,则( )  ,
,
 ,
, ,
, ,
,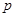 :函数
:函数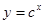 在
在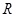 上单调递减,命题
上单调递减,命题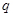 :不等式
:不等式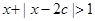 的解集为
的解集为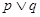 为真,
为真,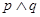 为假,求实数
为假,求实数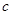 的取值范围.
的取值范围. 为真命题,则
为真命题,则 均为真命题
均为真命题 ,
, ”的否定是“
”的否定是“
 ,
,  ”
”  ”是“方程
”是“方程 表示椭圆”的充要条件
表示椭圆”的充要条件 ,使
,使 成立”是假命题,则实数
成立”是假命题,则实数 的取值范围为
的取值范围为 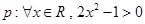 ,则该命题的否定是 。
,则该命题的否定是 。 ”是命题“
”是命题“ ”的必要非充分条件, 请写出一个满足条件的非空集合
”的必要非充分条件, 请写出一个满足条件的非空集合 .
.