题目内容
三棱锥S-ABC中SA⊥平面ABC,AB丄BC,SA=2,AB=BC=1,则三棱锥S-ABC的外接球的表面积等于
6π
6π
.分析:根据AB丄BC,AB=BC=1,可得外接球的球心O在过AC中点D且垂直于平面ABC的直线上,进而可计算三棱锥S-ABC的外接球的半径,由此可求三棱锥S-ABC的外接球的表面积.
解答:解:∵AB丄BC,AB=BC=1,
∴外接球的球心O在过AC中点D且垂直于平面ABC的直线上;
∵SA⊥平面ABC,AD=
,OD∥SA,
∴OA=
=
,
∴三棱锥S-ABC的外接球的表面积=4π×(
)2=6π
故答案为:6π
∴外接球的球心O在过AC中点D且垂直于平面ABC的直线上;
∵SA⊥平面ABC,AD=
| ||
| 2 |
∴OA=
(
|
| ||
| 2 |
∴三棱锥S-ABC的外接球的表面积=4π×(
| ||
| 2 |
故答案为:6π
点评:本题考查球的表面积的计算,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,SA=AB=AC=BC=
如图,在三棱锥S-ABC中,SA=AB=AC=BC=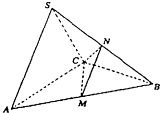 在三棱锥S-ABC中,△ABC是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,SA=
在三棱锥S-ABC中,△ABC是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,SA= 10、如图,在三棱锥S-ABC中,OA=OB,O为BC中点,SO⊥平面ABC,E为SC中点,F为AB中点.
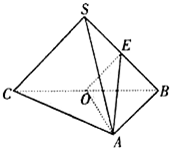
10、如图,在三棱锥S-ABC中,OA=OB,O为BC中点,SO⊥平面ABC,E为SC中点,F为AB中点.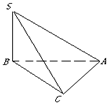 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: