题目内容
函数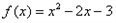 。定义数列
。定义数列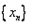 如下:
如下: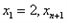 是过两点
是过两点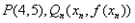 的直线
的直线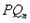 与x轴交点的横坐标。
与x轴交点的横坐标。
(1)证明: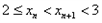 ;
;
(2)求数列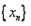 的通项公式。
的通项公式。
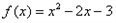 。定义数列
。定义数列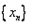 如下:
如下: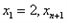 是过两点
是过两点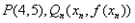 的直线
的直线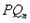 与x轴交点的横坐标。
与x轴交点的横坐标。(1)证明:
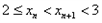 ;
;(2)求数列
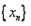 的通项公式。
的通项公式。解:(1)因为 ,
,
故点 在函数
在函数 的图像上,
的图像上,
故由所给出的两点 ,
,
可知,直线 斜率一定存在。
斜率一定存在。
故有直线 的直线方程为
的直线方程为 ,令
,令 ,
,
可求得
所以
下面用数学归纳法证明
当 时,
时, ,满足
,满足
假设 时,
时, 成立,
成立,
则当 时,
时, ,
,
由
即 也成立
也成立
综上可知 对任意正整数恒成立。
对任意正整数恒成立。
下面证明
由
由 ,
,
故有
即
综上可知 恒成立。
恒成立。
(2)由 得到该数列的一个特征方程
得到该数列的一个特征方程
 即
即 ,解得
,解得 或
或

 ①
①  ②
②
两式相除可得 ,而
,而
故数列 是以
是以 为首项以
为首项以 为公比的等比数列
为公比的等比数列

故 。
。
 ,
,故点
 在函数
在函数 的图像上,
的图像上,故由所给出的两点
 ,
,可知,直线
 斜率一定存在。
斜率一定存在。故有直线
 的直线方程为
的直线方程为 ,令
,令 ,
,可求得

所以

下面用数学归纳法证明

当
 时,
时, ,满足
,满足
假设
 时,
时, 成立,
成立,则当
 时,
时, ,
,由

即
 也成立
也成立综上可知
 对任意正整数恒成立。
对任意正整数恒成立。下面证明

由

由
 ,
,故有

即

综上可知
 恒成立。
恒成立。(2)由
 得到该数列的一个特征方程
得到该数列的一个特征方程 即
即 ,解得
,解得 或
或

 ①
①  ②
②两式相除可得
 ,而
,而
故数列
 是以
是以 为首项以
为首项以 为公比的等比数列
为公比的等比数列
故
 。
。
练习册系列答案
相关题目
 ,其中
,其中 .定义数列
.定义数列 如下:
如下: ,
, .
. 时,求
时,求 的值;
的值; 的值,若不存在,请说明理由;
的值,若不存在,请说明理由; 时,总能找到
时,总能找到 ,使得
,使得 .
.