题目内容
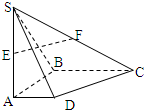 如图所示:在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,E、F分别为SA、SC的中点.如果AB=BC=2,AD=1,SB与底面ABCD成60°角.
如图所示:在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,E、F分别为SA、SC的中点.如果AB=BC=2,AD=1,SB与底面ABCD成60°角.(1)求异面直线EF与CD所成角的大小(用反三角形式表示);
(2)求点D到平面SBC的距离.
分析:(1)法一:连接AC,则∠ACD即为异面直线EF与CD所成角,然后利用余弦定理求出此角的余弦值,最后用反三角表示即可.
法二:以A为坐标原点,AD、BA、AS方向为正方向建立坐标系,求出异面直线EF与CD的方向向量,利用向量的夹角公式求出夹角即可;
(2)由于SA⊥平面ABCD,所以∠SBA即为斜线SB与底面ABCD所成角60°,然后根据等体积法建立等式关系
SBCD×SA=
S△SBC×h,求出h即为点D到平面SBC的距离.
法二:以A为坐标原点,AD、BA、AS方向为正方向建立坐标系,求出异面直线EF与CD的方向向量,利用向量的夹角公式求出夹角即可;
(2)由于SA⊥平面ABCD,所以∠SBA即为斜线SB与底面ABCD所成角60°,然后根据等体积法建立等式关系
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)连接AC,则∠ACD即为异面直线EF与CD所成角.
计算得:AC=2
,CD=
cos∠ACD=
,
所以异面直线 EF与CD成arccos
角.
另解:以A为坐标原点,AD、BA、AS方向为正方向建立坐标系
计算SA=2
=(1,-1,0)、
=(2,-1,0)
计算得cosα=
,所以异面直线 EF与CD成arccos
角
(2)由于SA⊥平面ABCD,所以∠SBA即为斜线SB与底面ABCD所成角60°
计算得:SA=2
,SB=4,S△SBC=4S△BCD=2
由于
SBCD×SA=
S△SBC×h
所以h=
计算得:AC=2
| 2 |
| 5 |
3
| ||
| 10 |
所以异面直线 EF与CD成arccos
3
| ||
| 10 |
另解:以A为坐标原点,AD、BA、AS方向为正方向建立坐标系
计算SA=2
| 3 |
| FE |
| CD |
计算得cosα=
3
| ||
| 10 |
3
| ||
| 10 |
(2)由于SA⊥平面ABCD,所以∠SBA即为斜线SB与底面ABCD所成角60°
计算得:SA=2
| 3 |
由于
| 1 |
| 3 |
| 1 |
| 3 |
所以h=
| 3 |
点评:本题主要考查了两异面直线所成角,以及利用等体积法求点到平面的距离,属于中档题.

练习册系列答案
相关题目
 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=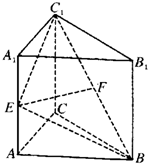 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°, ,BC=CC1=1,P是BC1上一动点,则
,BC=CC1=1,P是BC1上一动点,则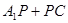 的最小值是_____.
的最小值是_____.

 ,AA1=6,E,F分别为AA1与BC1的中点.
,AA1=6,E,F分别为AA1与BC1的中点.