Question

已知函数f（x）=x|x-a|（a∈R）．
（I）判断f（x）的奇偶性；
（Ⅱ）解关于x的不等式：f（x）≥2a²；
（Ⅲ）写出f（x）的单调区间．

Answer 1

分析：（I）利用函数的奇偶性的定义直接判断即可；
（Ⅱ）直接表示出f（x）≥2a²，然后转化为不等式组求出解集即可．
（Ⅲ）通过对a的取值讨论，直接借助函数的图象求出f（x）的单调区间即可．

解答：解：（I）函数f （x ）的定义域是R，当a=0时，f （-x ）=-x|-x|=-x|x|=-f （x ），
∴f （x ）是奇函数．
当a≠0时，∵f （a ）=0，f （-a ）=-2a|a|，
∴f （-a ）≠f （a ）且f （-a ）≠-f （a ），
∴f （x ）既不是奇函数，也不是偶函数．
（II）∵x|x-a|≥2a²，
∴原不等式等价于

x＜a -x2+ax≥2a2

①或

x≥a x2-ax≥2a2

②
由①得

x＜a x2-ax+2a2≤0

，无解；
由②得

x≥a x2-ax-2a2≥0

，即

x≥a (x-2a)(x+a)≥0

，
（1）当a=0时，x≥0；
（2）当a＞0时，由

x≥a x≥2a或x≤-a

，得x≥2a．
（3）当a＜0时，由

x≥a x≥-a或x≤2a

，得x≥-a．
综上，当a≥0时，f （x ）≥2a²的解集为{x|x≥2a}；当a＜0时，f （x ）≥2a²的解集为{x|x≥-a}．
（III）f （x）=x|x-a|=

x2-ax，(x≥a) -x2+ax，(x＜a)

．
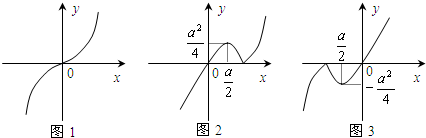
（1）a=0时，如图1，函数f （x ）在R上为单调递增函数，（-∞，+∞）为单调递增区间；
（2）a＞0时，如图2，函数f （x ）的单调递增区间为[a，+∞）和（-∞，

a

2

]，单调递减为[

a

2

，a]；
（3）a＜0时，如图2，函数f （x ）的单调递增区间为[

a

2

，+∞）和（-∞，a]，单调递减为[a，

a

2

]．

点评：本题考查函数的奇偶性，函数的图象的作法，分类讨论思想的应用，考查计算能力．