题目内容
在底面是直角梯形的四棱锥P—ABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA= AB=BC=2,AD=1,则D到平面PBC的距离为____________.
答案: 
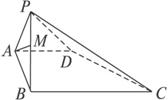
解析:∵BC∥AD,
∴点D到平面PBC的距离即为点A到平面PBC的距离.如图,取PB中点M,连结AM,由侧棱PA⊥底面ABCD,∠ABC=90°,
得CB⊥面PAB,
∴CB⊥AM.又AM⊥PB,
∴AM⊥面PBC.
,即为D到平面PBC的距离.
练习册系列答案
相关题目
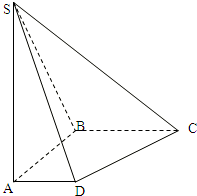如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=
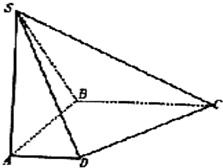如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，
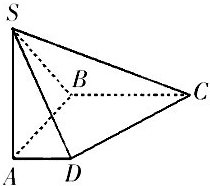如图在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，
如图，在底面是直角梯形的四棱锥S-ABCD中，已知∠ABC=90°，SA⊥平面ABCD，AB=BC=2，AD=1．
（2010•宝山区模拟）在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=