题目内容
在直角坐标系中,射线OA、OB的方程分别为x-y=0(x≥0),x+y=0(x≥0).动点P在∠AOB的内部,且点P到∠AOB的两边距离的平方差的绝对值等于1,求动点P的轨迹方程.

解析:设动点P的坐标为(x,y),过点P作PF⊥OA,作PE⊥OB,E、F分别为垂足,则点P属于集合M={P|||PE|2-|PF|2|=1},根据点到直线的距离公式,得
|(![]() )2-(
)2-(![]() )2|=1.
)2|=1.
化简,得|2xy|=1,即xy=±![]() .
.
又∵动点P在∠AOB内部,而曲线xy=±![]() 在x>0时并不全在∠AOB内部,故还需确定x的取值范围.
在x>0时并不全在∠AOB内部,故还需确定x的取值范围.
解方程组 得F(
得F(![]() ,
,![]() ).
).
解方程组 得F(
得F(![]() ,-
,-![]() ).
).
∴点P的轨迹方程为xy=±![]() (x≥
(x≥![]() ).?
).?
轨迹为双曲线xy=±![]() 在∠AOB内部的部分(含边界).
在∠AOB内部的部分(含边界).

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
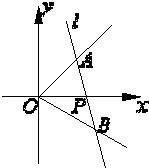 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: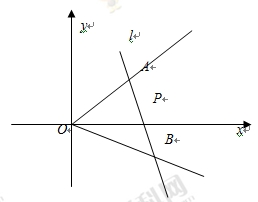
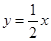 上时,求直线AB的方程.
上时,求直线AB的方程.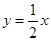 上时,求直线AB的方程.
上时,求直线AB的方程. :
: ,
, :
: ,
, 作直线分别交射线
作直线分别交射线 、
、 点.
点.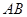 的中点为
的中点为 时,求直线
时,求直线 上时,求直线
上时,求直线