题目内容
已知椭圆E: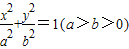 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: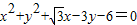 过A,F2两点.
过A,F2两点.(1)求椭圆E的方程;
(2)设直线PF2的倾斜角为α,直线PF1的倾斜角为β,当β-α=
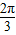 时,证明:点P在一定圆上.
时,证明:点P在一定圆上.(3)直线BC过坐标原点,与椭圆E相交于B,C,点Q为椭圆E上的一点,若直线QB,QC的斜率kQB,kQC存在且不为0,求证:kQB•kQC为定植.
【答案】分析:(1)求出圆与x轴交点坐标,即可确定椭圆E的方程;
(2)确定tanβ、tanα,利用两角差的正切公式,化简可得结论;
(3)求出直线QB,QC的斜率,利用点在椭圆上,代入作差,即可求得结论.
解答:(1)解:∵圆 与x轴交点坐标为
与x轴交点坐标为 ,
, ,
,
∴ ,∴b=3,
,∴b=3,
∴椭圆方程是: .…(4分)
.…(4分)
(2)证明:设点P(x,y),因为F1(- ,0),F2(
,0),F2( ,0),
,0),
所以 =tanβ=
=tanβ= ,
, =tanα=
=tanα= ,
,
因为β-α= ,所以tan(β-α)=-
,所以tan(β-α)=- .
.
因为tan(β-α)= =
= ,所以
,所以 =-
=- ,
,
化简得x2+y2-2y=3,所以点P在定圆x2+y2-2y=3上.…(10分)
(3)证明:设B(m,n),Q(x′,y′),则C(-m,-n)
∴kQB•kQC= =
=
∵ ,
,
∴两式相减可得
∴ =
=
∴kQB•kQC= …(12分)
…(12分)
点评:本题考查椭圆的标准方程,考查两角差的正切公式,考查斜率的计算,属于中档题.
(2)确定tanβ、tanα,利用两角差的正切公式,化简可得结论;
(3)求出直线QB,QC的斜率,利用点在椭圆上,代入作差,即可求得结论.
解答:(1)解:∵圆
 与x轴交点坐标为
与x轴交点坐标为 ,
, ,
,∴
 ,∴b=3,
,∴b=3,∴椭圆方程是:
 .…(4分)
.…(4分)(2)证明:设点P(x,y),因为F1(-
 ,0),F2(
,0),F2( ,0),
,0),所以
 =tanβ=
=tanβ= ,
, =tanα=
=tanα= ,
,因为β-α=
 ,所以tan(β-α)=-
,所以tan(β-α)=- .
.因为tan(β-α)=
 =
= ,所以
,所以 =-
=- ,
,化简得x2+y2-2y=3,所以点P在定圆x2+y2-2y=3上.…(10分)
(3)证明:设B(m,n),Q(x′,y′),则C(-m,-n)
∴kQB•kQC=
 =
=
∵
 ,
,
∴两式相减可得

∴
 =
=
∴kQB•kQC=
 …(12分)
…(12分)点评:本题考查椭圆的标准方程,考查两角差的正切公式,考查斜率的计算,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: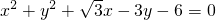 过A,F2两点.
过A,F2两点. 时,证明:点P在一定圆上.
时,证明:点P在一定圆上.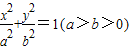 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: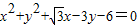 过A,F2两点.
过A,F2两点.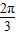 时,证明:点P在一定圆上.
时,证明:点P在一定圆上.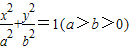 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: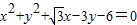 过A,F2两点.
过A,F2两点.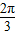 时,证明:点P在一定圆上.
时,证明:点P在一定圆上.