题目内容
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足
 =1-
=1- ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.
【答案】分析:(Ⅰ)设等差数列{an}的首项为a1,公差为d,由S4=4S2,a2n=2an+1得到关于a1与d的方程组,解之即可求得数列{an}的通项公式;
(Ⅱ)由(Ⅰ)知,an=2n-1,继而可求得bn=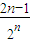 ,n∈N*,于是Tn=
,n∈N*,于是Tn= +
+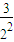 +
+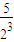 +…+
+…+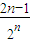 ,利用错位相减法即可求得Tn.
,利用错位相减法即可求得Tn.
解答:解:(Ⅰ)设等差数列{an}的首项为a1,公差为d,由S4=4S2,a2n=2an+1得: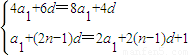 ,
,
解得a1=1,d=2.
∴an=2n-1,n∈N*.
(Ⅱ)由已知 +
+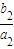 +…+
+…+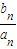 =1-
=1-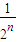 ,n∈N*,得:
,n∈N*,得:
当n=1时,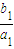 =
= ,
,
当n≥2时,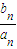 =(1-
=(1-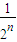 )-(1-
)-(1-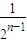 )=
)=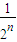 ,显然,n=1时符合.
,显然,n=1时符合.
∴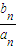 =
=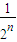 ,n∈N*
,n∈N*
由(Ⅰ)知,an=2n-1,n∈N*.
∴bn=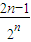 ,n∈N*.
,n∈N*.
又Tn= +
+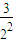 +
+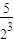 +…+
+…+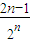 ,
,
∴ Tn=
Tn=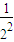 +
+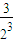 +…+
+…+ +
+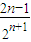 ,
,
两式相减得: Tn=
Tn= +(
+( +
+ +…+
+…+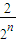 )-
)-
= -
- -
-
∴Tn=3-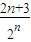 .
.
点评:本题考查数列递推式,着重考查等差数列的通项公式与数列求和,突出考查错位相减法求和,考查分析运算能力,属于中档题.
(Ⅱ)由(Ⅰ)知,an=2n-1,继而可求得bn=
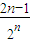 ,n∈N*,于是Tn=
,n∈N*,于是Tn= +
+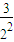 +
+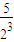 +…+
+…+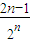 ,利用错位相减法即可求得Tn.
,利用错位相减法即可求得Tn.解答:解:(Ⅰ)设等差数列{an}的首项为a1,公差为d,由S4=4S2,a2n=2an+1得:
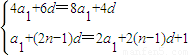 ,
,解得a1=1,d=2.
∴an=2n-1,n∈N*.
(Ⅱ)由已知
 +
+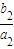 +…+
+…+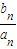 =1-
=1-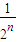 ,n∈N*,得:
,n∈N*,得:当n=1时,
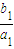 =
= ,
,当n≥2时,
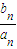 =(1-
=(1-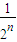 )-(1-
)-(1-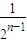 )=
)=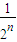 ,显然,n=1时符合.
,显然,n=1时符合.∴
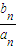 =
=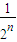 ,n∈N*
,n∈N*由(Ⅰ)知,an=2n-1,n∈N*.
∴bn=
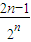 ,n∈N*.
,n∈N*.又Tn=
 +
+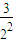 +
+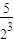 +…+
+…+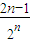 ,
,∴
 Tn=
Tn=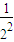 +
+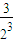 +…+
+…+ +
+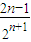 ,
,两式相减得:
 Tn=
Tn= +(
+( +
+ +…+
+…+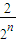 )-
)-
=
 -
- -
-
∴Tn=3-
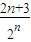 .
.点评:本题考查数列递推式,着重考查等差数列的通项公式与数列求和,突出考查错位相减法求和,考查分析运算能力,属于中档题.

练习册系列答案
相关题目