题目内容
设O是平面ABC外一点,点M满足条件
=
+
+
,则直线AM( )
| OM |
| 3 |
| 4 |
| OA |
| 1 |
| 8 |
| OB |
| 1 |
| 8 |
| OC |
| A.与平面ABC平行 | B.是平面ABC的斜线 |
| C.是平面ABC的垂线 | D.在平面ABC内 |
∵
=
+
+
∴由
=
+
+
,得
+
+
=
+
+
移项,得
(
-
)=
(
-
)+
(
-
)
∴
=
+
,即
=-
-
由此可得向量
、
、
是共面向量,由此可得直线AM在平面ABC内
故选:D
| OM |
| 3 |
| 4 |
| OM |
| 1 |
| 8 |
| OM |
| 1 |
| 8 |
| OM |
∴由
| OM |
| 3 |
| 4 |
| OA |
| 1 |
| 8 |
| OB |
| 1 |
| 8 |
| OC |
| 3 |
| 4 |
| OM |
| 1 |
| 8 |
| OM |
| 1 |
| 8 |
| OM |
| 3 |
| 4 |
| OA |
| 1 |
| 8 |
| OB |
| 1 |
| 8 |
| OC |
移项,得
| 3 |
| 4 |
| OM |
| OA |
| 1 |
| 8 |
| OB |
| OM |
| 1 |
| 8 |
| OC |
| OM |
∴
| 3 |
| 4 |
| AM |
| 1 |
| 8 |
| MB |
| 1 |
| 8 |
| MC |
| MA |
| 1 |
| 6 |
| MB |
| 1 |
| 6 |
| MC |
由此可得向量
| MA |
| MB |
| MC |
故选:D

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足
在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足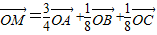 ,则直线AM( )
,则直线AM( )