题目内容
曲线 与直线y=k(x-1)+5有两个不同交点时,实数k的取值范围是________.
与直线y=k(x-1)+5有两个不同交点时,实数k的取值范围是________.

分析:由题意可得,曲线表示一个半圆,直线过定点M(0,5),先求出切线MD、ME的斜率,再求出MA、MB的斜率,数形结合可得曲线与半圆有两个不同交点时,实数k的取值范围.
解答:
 解:曲线
解:曲线 ,即 (x-1)2+(y-2)2=4,(y≥2),表示一个半圆.
,即 (x-1)2+(y-2)2=4,(y≥2),表示一个半圆.直线y=k(x-1)+5=kx+5-k 过定点M(1,5),如图所示:A(-1,2)、B(3,2).
当直线和半圆相切时,则圆心C(1,2)到直线kx-y+5-k=0的距离等于半径,即
 =2,
=2,解得 k=±
 ,即切线MA的斜率为
,即切线MA的斜率为 ,切线MB的斜率为-
,切线MB的斜率为- .
.由于MA的斜率为
 =
= ,MB的斜率等于
,MB的斜率等于  =-
=- ,
,数形结合可得,当直线和半圆有两个不同交点时,实数k的取值范围是
 ,
,故答案为
 .
.点评:本题主要考查直线和圆相交的性质,直线过定点问题,直线的斜率公式的应用,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
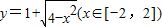 与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )
与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )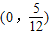
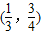
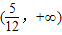
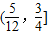
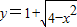 与直线y=k(x-2)+4有两个交点,则实数k的取值范围为 .
与直线y=k(x-2)+4有两个交点,则实数k的取值范围为 . 与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )
与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )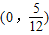
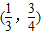
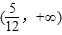
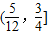
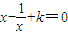 在x∈(0,1)没有实数根,则k的取值范围是k≥2
在x∈(0,1)没有实数根,则k的取值范围是k≥2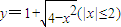 与直线y=k(x-2)+4有两个交点时,实数k的取值范围是
与直线y=k(x-2)+4有两个交点时,实数k的取值范围是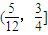
 的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是
的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是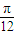 ,其中正确的结论是: .
,其中正确的结论是: . 与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )
与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )


