题目内容
设 的定义域为D,若
的定义域为D,若 满足下面两个条件,则称
满足下面两个条件,则称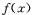 为闭函数.①
为闭函数.① 在D内是单调函数;②存在
在D内是单调函数;②存在 ,使f(x)在[a,b]上的值域为[a,b].如果
,使f(x)在[a,b]上的值域为[a,b].如果 为闭函数,那么k的取值范围是
为闭函数,那么k的取值范围是
 的定义域为D,若
的定义域为D,若 满足下面两个条件,则称
满足下面两个条件,则称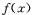 为闭函数.①
为闭函数.① 在D内是单调函数;②存在
在D内是单调函数;②存在 ,使f(x)在[a,b]上的值域为[a,b].如果
,使f(x)在[a,b]上的值域为[a,b].如果 为闭函数,那么k的取值范围是
为闭函数,那么k的取值范围是| A.k<l | B. | C.k >-1 | D.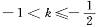 |
D
方法一: 在定义域
在定义域 上单调递增,则
上单调递增,则 。根据单调性可知当
。根据单调性可知当 时,
时, 。由闭函数的定义可得,
。由闭函数的定义可得, ,故
,故 是方程
是方程 即
即 在
在 的两根,所以
的两根,所以
 ,解得
,解得
因为 ,所以
,所以 ,故有
,故有
综上可得, ,故选D。
,故选D。
方法二: 在定义域
在定义域 上单调递增,根据闭函数的定义可得
上单调递增,根据闭函数的定义可得 ,所以
,所以 即
即 在
在 上有两个不同的实根,由此可以将问题转化为函数
上有两个不同的实根,由此可以将问题转化为函数 和
和 在
在 上有两个不同的交点
上有两个不同的交点
函数图象如下:

当直线 位于临界直线m位置时,可得函数
位于临界直线m位置时,可得函数 和
和 在坐标轴上的交点相同,从而有
在坐标轴上的交点相同,从而有 ,则
,则
当直线 位于临界直线n位置时,
位于临界直线n位置时, 与
与 相切。
相切。
 ,令
,令 可得
可得 ,从而可知切点坐标为
,从而可知切点坐标为 ,所以
,所以
综上可得, ,故选D。
,故选D。
 在定义域
在定义域 上单调递增,则
上单调递增,则 。根据单调性可知当
。根据单调性可知当 时,
时, 。由闭函数的定义可得,
。由闭函数的定义可得, ,故
,故 是方程
是方程 即
即 在
在 的两根,所以
的两根,所以 ,解得
,解得
因为
 ,所以
,所以 ,故有
,故有
综上可得,
 ,故选D。
,故选D。方法二:
 在定义域
在定义域 上单调递增,根据闭函数的定义可得
上单调递增,根据闭函数的定义可得 ,所以
,所以 即
即 在
在 上有两个不同的实根,由此可以将问题转化为函数
上有两个不同的实根,由此可以将问题转化为函数 和
和 在
在 上有两个不同的交点
上有两个不同的交点函数图象如下:

当直线
 位于临界直线m位置时,可得函数
位于临界直线m位置时,可得函数 和
和 在坐标轴上的交点相同,从而有
在坐标轴上的交点相同,从而有 ,则
,则
当直线
 位于临界直线n位置时,
位于临界直线n位置时, 与
与 相切。
相切。 ,令
,令 可得
可得 ,从而可知切点坐标为
,从而可知切点坐标为 ,所以
,所以
综上可得,
 ,故选D。
,故选D。
练习册系列答案
相关题目
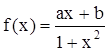 是定义在
是定义在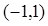 上的奇函数,且
上的奇函数,且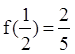
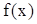 的解析式。
的解析式。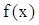 在
在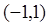 上是增函数。
上是增函数。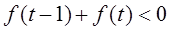
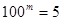 ,
,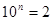 ,
,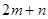 的值.
的值.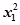 )+f(
)+f(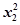 )+…+f(
)+…+f(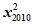 )的值
)的值
 ,在
,在 处的
处的 .
. 的解析式;
的解析式;
 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. , x
, x ,x
,x
 R,且x
R,且x 在区间
在区间
 为整数)上的值域是
为整数)上的值域是 ,则满足条件的数对
,则满足条件的数对 共有 ▲ 对;
共有 ▲ 对; 的方程组
的方程组 有两组不同的解,则实数
有两组不同的解,则实数 的取值范围是____________.
的取值范围是____________. ,
, ,则
,则 的取值范围是_________________.
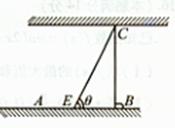
的取值范围是_________________.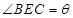 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为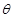 的函数;并求自变量
的函数;并求自变量