题目内容
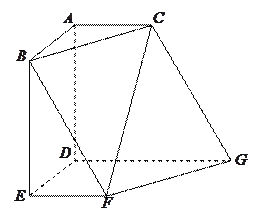
【题目】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
,
![]()
![]() 为
为![]() 中点.
中点.

(Ⅰ)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(Ⅱ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,请说明点
,若存在,请说明点![]() 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)设![]() 为
为![]() 中点,利用三角形中位线定理及其线面平行的判定定理可得截面如图所示;(Ⅱ)建立空间直角坐标系,设在线段
中点,利用三角形中位线定理及其线面平行的判定定理可得截面如图所示;(Ⅱ)建立空间直角坐标系,设在线段![]() 上存在一点
上存在一点![]() ,求出面
,求出面![]() 的法向量,利用
的法向量,利用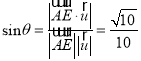 可得解;(Ⅲ)求出平面
可得解;(Ⅲ)求出平面![]() 的法向量,求出法向量的夹角即可.
的法向量,求出法向量的夹角即可.
试题解析:(Ⅰ)解:作PB的中点N,连接MN,如图,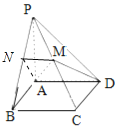
(在图中画出)因此,N为PB的中点.
(Ⅱ)因为四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,以A为坐标原点,以直线AB,AD,AP所在直线建立空间直角坐标系如图所示:则
,以A为坐标原点,以直线AB,AD,AP所在直线建立空间直角坐标系如图所示:则
![]()
设在线段![]() 上存在一点
上存在一点![]() ,则
,则![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
则![]()
即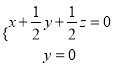 令
令![]() ,则
,则![]()
则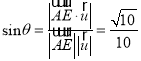 ,所以
,所以![]()
所以在线段![]() 上存在中点
上存在中点![]() ,
,
使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)设平面![]() 的法向量
的法向量![]() ,则
,则![]()
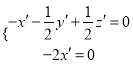 令
令![]() ,则
,则![]() ,所以
,所以![]()
所以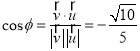
所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(万元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求:
(1)求![]() ; (2)线性回归方程
; (2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式: