题目内容
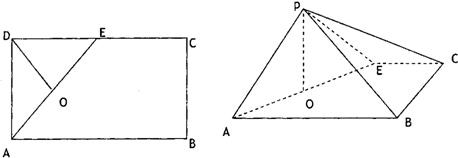
如图所示,在矩形ABCD中,AB=2BC=2a,E为AB上的一点,将B点沿线段EC折起至点P,连接PA、PC、PD,取PD中点F,且AF∥平面PEC.(1)确定点E的位置;
(2)若异面直线PE、CD成60°角,求证:平面PEC⊥平面AECD;
(3)在(2)的条件下求点F到平面PEC的距离.

第19题图
答案:(1)设平面AEF交直线PC于M,因为AF∥平面PEC,所以AF∥EM,
又因为AE∥平面PDC,所以AE∥FM,
因为F是PD中点,所以M是PC中点,AE=FM=![]() CD,因此E是AB的中点.
CD,因此E是AB的中点.

第19题图
(2)取CE中点K,连接PK、BK,则PK=BK=![]() a,
a,
若∠PEB=120°,则PB=![]() 大于PK与BK之和,这不可能.
大于PK与BK之和,这不可能.
所以∠PEB=60°,∴PB=a,∴△PKB为直角三角形
∴PK⊥BK,又∵PK⊥EC,∴PK⊥平面AECD
∴平面PEC⊥平面AECD.
(3)因为点F到平面PEC的距离等于点D到平面PEC的距离的一半,易证DE⊥平面PEC,DE=![]() a
a
∴点F到平面PEC的距离为![]() .
.

练习册系列答案
相关题目
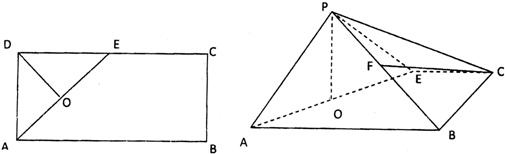 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
 如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是
如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为