题目内容
给出下列各对函数:①
 ;
;②f(x)=2x+1,g(x)=2x-1;
③
 ;
;④
 ,其中是同一函数的是 (写出所有符合要求的函数序号)
,其中是同一函数的是 (写出所有符合要求的函数序号)
【答案】分析:在①、③中,由于两个函数的定义域不同,故不是同一个函数.在②中,由于两个函数的对应关系不同,故不是同一个函数.④中这两个函数的三要素全部相同,故是同一个函数.
解答:解:在①中, 的定义域为R,
的定义域为R, 的定义域为{x|x≥0},
的定义域为{x|x≥0},
这两个函数的定义域,故不是同一个函数.
在②中,f(x)=2x+1和g(x)=2x-1的对应关系不同,故不是同一个函数.
在③中, 的定义域为{x|x>1},
的定义域为{x|x>1}, 的定义域为{x|x>1或x<-1},
的定义域为{x|x>1或x<-1},
这两个函数的定义域,故不是同一个函数.
在④中,f(x)=2-x= =g(x),这两个函数具有相同的定义域、对应关系、值域,故是同一个函数.
=g(x),这两个函数具有相同的定义域、对应关系、值域,故是同一个函数.
故答案为 ④.
点评:本题主要考查函数的三要素,两个函数是同一个函数,当且仅当这两个函数具有相同的定义域、值域、对应关系.
解答:解:在①中,
 的定义域为R,
的定义域为R, 的定义域为{x|x≥0},
的定义域为{x|x≥0},这两个函数的定义域,故不是同一个函数.
在②中,f(x)=2x+1和g(x)=2x-1的对应关系不同,故不是同一个函数.
在③中,
 的定义域为{x|x>1},
的定义域为{x|x>1}, 的定义域为{x|x>1或x<-1},
的定义域为{x|x>1或x<-1},这两个函数的定义域,故不是同一个函数.
在④中,f(x)=2-x=
 =g(x),这两个函数具有相同的定义域、对应关系、值域,故是同一个函数.
=g(x),这两个函数具有相同的定义域、对应关系、值域,故是同一个函数.故答案为 ④.
点评:本题主要考查函数的三要素,两个函数是同一个函数,当且仅当这两个函数具有相同的定义域、值域、对应关系.

练习册系列答案
相关题目
 ,②
,②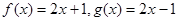 ,③
,③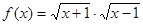
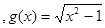 ,④
,④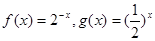 ,其中是同一函数的是______________(写出所有符合要求的函数序号)
,其中是同一函数的是______________(写出所有符合要求的函数序号)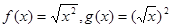 ,②
,②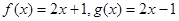 ,③
,③
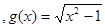 ,④
,④ ,其中是同一函数的是_________(写出所有符合要求的函数序号)
,其中是同一函数的是_________(写出所有符合要求的函数序号)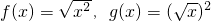 ;
;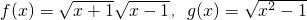 ;
;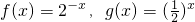 ,
,