题目内容
如图,已知A,B,C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且(1)求椭圆方程;
(2)过点D(0,2)的直线l与椭圆相交于不同的两点M,N且M在D,N之间,设![]() =λ
=λ![]() ,求实数λ的取值范围.?
,求实数λ的取值范围.?
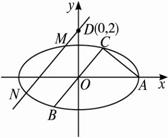
解:(1)设A(2,0),则椭圆方程为![]() =1. ?
=1. ?
∵O为椭圆中心,?
∴由对称性知|OC|=|OB|.?
又∵![]() ·
·![]() =0,∴AC⊥BC.?
=0,∴AC⊥BC.?
又∵|BC|=2|AC|,∴|OC|=|AC|.?
∴△AOC为等腰直角三角形. ?
∴点C的坐标为(1,1).?
∴点B的坐标为(-1,-1).?
将C的坐标(1,1)代入椭圆方程得b2=![]() , ?
, ?
则求得椭圆的方程为![]() =1. ?
=1. ?
(2)∵M在D,N之间,∴λ>0. ?
设M(x1,y1),N(x2,y2),则x1=![]() ,y1=
,y1=![]() , ?
, ?
∵M,N在椭圆上,∴x12+3y12=4,x22+3y22=4.?
∴(![]() )2+(
)2+(![]() )2=4
)2=4![]() λ2(x22+3y22)+12λy2+12=4λ2+8λ+4,?
λ2(x22+3y22)+12λy2+12=4λ2+8λ+4,?
即3λy2+2=2λ![]() y2=
y2=![]() . ?
. ?
∴-![]() ≤y2≤
≤y2≤![]() .?
.?
∴-![]() ≤
≤![]() ≤
≤![]() . ?
. ?
解得λ≥![]() ,?
,?
∴实数λ的取值范围是[![]() ,+∞).
,+∞).

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案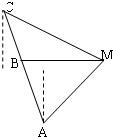 如图,已知A、B、C是一条直路上的三点,AB与BC各等于1千米,从三点分别遥望塔M,在A处看见塔在北偏东45方向,在B处看见塔在正东方向,在C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
如图,已知A、B、C是一条直路上的三点,AB与BC各等于1千米,从三点分别遥望塔M,在A处看见塔在北偏东45方向,在B处看见塔在正东方向,在C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离. 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC. 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且