Question

（本小题共13分）

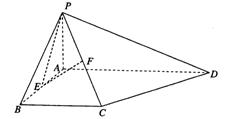
        如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=

∠BAD=90°，为AB中点，F为PC中点.

   （I）求证：PE⊥BC；

   （II）求二面角C—PE—A的余弦值；

   （III）若四棱锥P—ABCD的体积为4，求AF的长.

Answer 1

（本题满分13分）

解：（I）

∴PA⊥BC

∴BC⊥平面PAB

又E是AB中点，

平面PAB

∴BC⊥PE.                  …………6分

   （II）建立直角坐标系

则B（1，0，0），C（1，1，0），P（0，0，1），

由（I）知，BC⊥平面PAE，

是平面PAE的法向量.

设平面PEC的法向量为

则

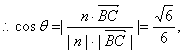
二面角C—PE—A的余弦值为              …………10分

   （III）连结BC，设AB=a，

   

是直角三角形，

         …………13分