Question

20．若一个正三棱台的侧梭长为5，上、下底面边长分别为4和10，则其斜高等于（　　）

• A． 3
• B． 4
• C． $\sqrt{34}$
• D． $\sqrt{11}$

Answer 1

分析 M、N分别为上下底面的中心，取上下底面边的中点H和P，则HP为侧面的斜高，根据图求出斜高的值．

解答 解：如图所示，正三棱台的侧棱长AD=5，上、下底面边长分别为DE=4，AB=10，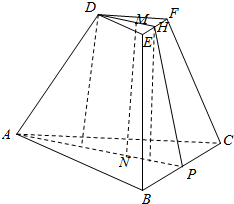

连接上下底面的中心MN，则MN是棱台的高，
取EF的中点H，BC的中点P，连接PH，则PH是斜高；
∴DH=$\frac{\sqrt{3}}{2}$DE=2$\sqrt{3}$，AP=$\frac{\sqrt{3}}{2}$AB=5$\sqrt{3}$，
∴DM=$\frac{2}{3}$DE=$\frac{4\sqrt{3}}{3}$，AN=$\frac{2}{3}$AP=$\frac{10\sqrt{3}}{3}$，
∴MN=$\sqrt{{5}^{2}{-（\frac{10\sqrt{3}}{3}-\frac{4\sqrt{3}}{3}）}^{2}}$=$\sqrt{13}$；
又MH=$\frac{1}{3}$DH=$\frac{2\sqrt{3}}{3}$，NP=$\frac{1}{3}$AP=$\frac{5\sqrt{3}}{3}$，
∴HP=$\sqrt{{（\sqrt{13}）}^{2}{+（\frac{5\sqrt{3}}{3}-\frac{2\sqrt{3}}{3}）}^{2}}$=4；即斜高为4．
故选：B．

点评 本题考查了三棱台的结构特征与量的计算问题，是中档题目．