题目内容
已知向量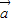
=（1，2），
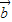=（-2，m），m∈R．（Ⅰ）若
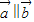，求m的值；（Ⅱ）若
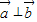，求m的值．
【答案】分析：（I）利用向量共线的坐标表示即可得出；
（II）利用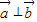
?
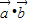=0，即可得出．
解答：解（Ⅰ）因为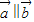
，
所以1•m-2（-2）=0，m=-4．
（Ⅱ）因为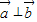
，所以
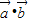=0，
所以1•（-2）+2m=0，m=1．
点评：熟练掌握向量共线与垂直的坐标表示是解题的关键．
（II）利用
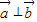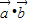?=0，即可得出．解答：解（Ⅰ）因为
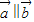，所以1•m-2（-2）=0，m=-4．
（Ⅱ）因为
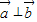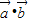，所以=0，所以1•（-2）+2m=0，m=1．
点评：熟练掌握向量共线与垂直的坐标表示是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
已知向量
=（1，2），
=（x，2），则向量
+2
与2
-
（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、垂直的必要条件是x=-2 | ||
B、垂直的充要条件是x=
| ||
| C、平行的充分条件是x=-2 | ||
| D、平行的充要条件是x=1 |