题目内容
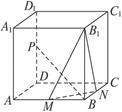
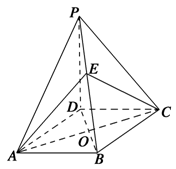
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(I)求证:A1C⊥平面BCDE;
(II)若M是A1D的中点,求CM与平面A1BE所成角的大小;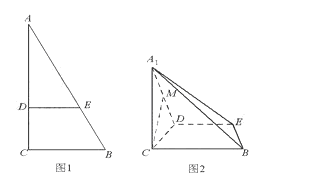
(I)先证 (II)
(II)
解析试题分析:(1) ,
,
 平面
平面 ,
,
又 平面
平面 ,
,

又 ,
, 平面
平面 。
。
(2)如图建系 ,则
,则 ,
, ,
, ,
,
∴ ,
,

设平面 法向量为
法向量为
则 ∴
∴ ∴
∴
∴
又∵
∴
∴ ,
,
∴ 与平面
与平面 所成角的大小
所成角的大小 .
.
考点:线面垂直 线面角
点评:本题考查线面垂直,考查线面角,考查面面垂直,既有传统方法,又有向量知识的运用,要加以体会.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
过点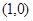 且与直线
且与直线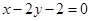 平行的直线方程是( )
平行的直线方程是( )
A. | B. |
C. | D. |
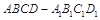 ,中,
,中,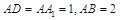 ,点
,点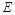 在棱AB上移动.
在棱AB上移动.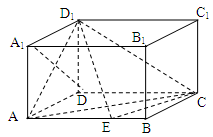
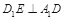 ;
; 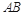 的中点时,求点
的中点时,求点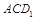 的距离;
的距离; 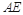 等于何值时,二面角
等于何值时,二面角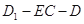 的大小为
的大小为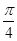 .
. 的底边
的底边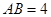 ,点
,点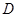 在线段
在线段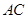 上,
上,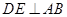 于
于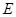 ,现将
,现将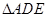 沿
沿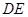 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
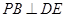 ;
;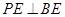 ,直线
,直线 与平面
与平面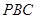 所成的角为
所成的角为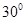 ,求
,求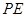 长.
长.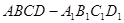 的棱长为
的棱长为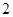 ,
,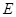 、
、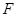 分别是
分别是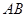 、
、 的中点.
的中点.
 的体积;
的体积;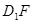 与平面
与平面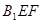 所成角的余弦值.
所成角的余弦值. 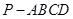 中,顶点
中,顶点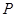 在底面
在底面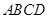 内的射影恰好落在
内的射影恰好落在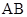 的中点
的中点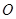 上,又
上,又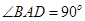 ,
,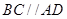 且
且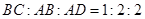
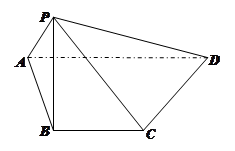
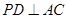 ;
;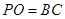 ,求直线
,求直线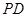 与
与 所成角的余弦值;
所成角的余弦值;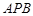 与平面
与平面 所成的角为
所成的角为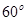 ,求
,求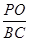 的值。
的值。