题目内容
已知锐角△ABC中，内角A、B、C的对边分别为a、b、c，向量
=(sinB，
ac)，
=(b 2-a2-c2，cosB)，且
⊥
（1）求角B的大小；
（2）求sin(B-50°)•[1+
tan(B+10°)]的值．
| m |
| 3 |
| n |
| m |
| n． |
（1）求角B的大小；
（2）求sin(B-50°)•[1+
| 3 |
分析：（1）根据
•
=0，利用向量数量积的坐标运算公式与余弦定理化简，可得accosB（
-2sinB）=0．再由△ABC是锐角三角形，算出sinB=
，从而可得B=60°；
（2）由（1）将B=60°代入，可得原式=sin10°（1+
tan70°）．再根据同角三角函数的关系、诱导公式与辅助角公式，化简得1+
tan70°=
，代入原式并利用二倍角的正弦公式加以计算，可得答案．
| m |
| n |
| 3 |
| ||
| 2 |
（2）由（1）将B=60°代入，可得原式=sin10°（1+
| 3 |
| 3 |
| 2cos10° |
| cos70° |
解答：解：（1）∵
=(sinB，
ac)，
=(b 2-a2-c2，cosB)，且
⊥
∴
•
=sinB（b2-a2-c2）+
accosB=0，
又∵△ABC中，根据余弦定理得b2=a2+c2-2accosB，可得b2-a2-c2=-2accosB，
∴-2acsinBcosB+
accosB=0，即accosB（
-2sinB）=0．
∵锐角△ABC中，accosB＞0，
∴
-2sinB=0，可得sinB=
，锐角B=60°；
（2）sin(B-50°)•[1+
tan(B+10°)]=sin10°（1+
tan70°）
∵1+
tan70°=1+
•
=
=
=
=
=
，
∴sin10°（1+
tan70°）=
=
=
=
=1．
因此，sin(B-50°)•[1+
tan(B+10°)]的值为1．
| m |
| 3 |
| n |
| m |
| n． |
∴
| m |
| n |
| 3 |
又∵△ABC中，根据余弦定理得b2=a2+c2-2accosB，可得b2-a2-c2=-2accosB，
∴-2acsinBcosB+
| 3 |
| 3 |
∵锐角△ABC中，accosB＞0，
∴
| 3 |
| ||
| 2 |
（2）sin(B-50°)•[1+
| 3 |
| 3 |
∵1+
| 3 |
| 3 |
| sin70° |
| cos70° |
| ||
| cos70° |
=
| 2sin(70°+30°) |
| cos70° |
| 2sin100° |
| cos70° |
| 2sin(90°+10°) |
| cos70° |
| 2cos10° |
| cos70° |
∴sin10°（1+
| 3 |
| 2sin10°cos10° |
| cos70° |
| sin20° |
| cos70° |
| sin(90°-70°) |
| cos70° |
| cos70° |
| cos70° |
因此，sin(B-50°)•[1+
| 3 |
点评：本题以向量数量积运算为载体，着重考查了同角三角函数的关系与诱导公式、二倍角的正弦公式与辅助角公式，考查了利用余弦定理解三角形的知识，属于中档题．
练习册系列答案
相关题目
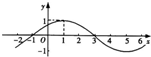已知函数f（x）=Asin（ωx+φ）（其中x∈R，A?＞0，ω＞0，