题目内容
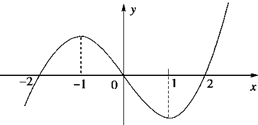
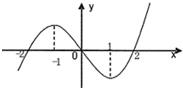
已知R上可导函数f(x)的图象如图所示,则不等式(x2﹣2x﹣3)f′(x)<0的解集 .
考点:
导数的运算;函数的图象.
专题:
导数的综合应用.
分析:
由f(x)的图象可知:当x<﹣1或x>1时,函数f(x)单调递增,f′(x)>0;当﹣1<x<1时,函数f(x)单调递减,f′(x)<0.
不等式(x2﹣2x﹣3)f′(x)<0可化为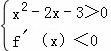 或
或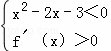 解出即可.
解出即可.
解答:
解:由f(x)的图象可知:当x<﹣1或x>1时,函数f(x)单调递增,∴f′(x)>0;当﹣1<x<1时,函数f(x)单调递减,f′(x)<0.
不等式(x2﹣2x﹣3)f′(x)<0可化为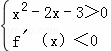 或
或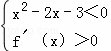
化为![]() 或
或![]() ,
,
解得∅或1<x<3.
∴不等式(x2﹣2x﹣3)f′(x)<0的解集是(1,3).
故答案为(1,3).
点评:
熟练掌握函数的单调性与当时的关系、不等式的解法、数形结合的思想方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 9、已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( )
9、已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( ) 已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)<0的解集
已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)<0的解集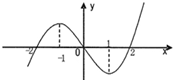 已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( )
已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( )