题目内容
设α,β,γ是三个互不重合的平面,l是直线,给出下列命题:①若α⊥β,β⊥γ,则α⊥γ;
②若α∥β,l∥β,则l∥α;
③若l⊥α,l∥β,则α⊥β;
④若α∥β,α⊥γ,则β⊥γ.
其中正确的命题是( )
A.①②
B.②③
C.②④
D.③④
【答案】分析:①利用面面垂直的性质定理去证明.②利用线面平行和面面平行的性质定理去判断.
③利用线面垂直和线面平行的性质去判断.④利用面面平行和面面垂直的性质取判断.
解答:解:①两平面都垂直于同一个平面,两平面可能平行可能相交,不一定垂直,故①错误.
②当直线l?α时,满足条件,但结论不成立.当直线l?α时,满足条件,此时有l∥α,所以②错误.
③平行于同一直线的两个平面平行,所以③正确.
④一个平面垂直于两平行平面中的一个必垂直于另一个.所以④正确.所以正确的命题为③④.
故选D.
点评:本题为命题真假的判断,正确认识空间里直线与平面的位置关系是解决问题的关键.
③利用线面垂直和线面平行的性质去判断.④利用面面平行和面面垂直的性质取判断.
解答:解:①两平面都垂直于同一个平面,两平面可能平行可能相交,不一定垂直,故①错误.
②当直线l?α时,满足条件,但结论不成立.当直线l?α时,满足条件,此时有l∥α,所以②错误.
③平行于同一直线的两个平面平行,所以③正确.
④一个平面垂直于两平行平面中的一个必垂直于另一个.所以④正确.所以正确的命题为③④.
故选D.
点评:本题为命题真假的判断,正确认识空间里直线与平面的位置关系是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
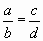 ,则a+d与b+c的大小关系是
,则a+d与b+c的大小关系是