Question

【题目】和平面解析几何的观点相同，在空间中，空间平面和曲面可以看作是适合某种条件的动点的轨迹，在空间直角坐标系中，空间平面和曲面的方程是一个三原方程.

（1）类比平面解析几何中直线的方程，写出①过点，法向量为的平面的点法式方程；②平面的一般方程；③在，，轴上的截距分别为，，的平面的截距式方程.（不需要说明理由）

（2）设、为空间中的两个定点，，我们将曲面定义为满足的动点的轨迹，试建立一个适当的空间直角坐标系，求曲面的方程.

（3）对（2）中的曲面，指出和证明曲面的对称性，并画出曲面的直观图.

Answer 1

【答案】（1）①；②；③

（2）

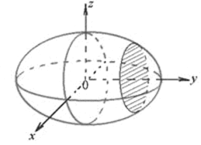
（3）关于原点对称，关于，，轴对称，关于，，平面对称，如图

【解析】

(1)类比平面中直线的点斜式方程,直线的一般方程,直线的截距式方程即可.

(2)类比平面中的求轨迹方程的方法,设空间中的点,再根据题意列出方程式化简求解即可.

(3)根据曲面方程可判断曲面关于原点对称,关于,,轴对称,关于,,平面对称再证明画出图像即可.

(1) 类比平面中直线的点斜式方程,直线的一般方程,直线的截距式方程可得：

①；②；③

(2) 以两个定点的中点为坐标原点,以所在的直线为轴,以线段的垂直平分线为轴,以与平面垂直的直线为轴,建立空间直角坐标系,

则,,设,可得,.

所以.

移项得

两边平方,得

∴

两边平方得

即,两边同除以,设则

.

因此,可得曲面Γ的方程为.

(3)由于点关于坐标原点的对称点也满足Γ的方程,

说明曲面Γ关于坐标原点对称；

由于点关于x轴的对称点也满足Γ的方程,

说明曲面Γ关于x轴对称；同理,曲面Γ关于y轴对称；关于z轴对称.

由于点关于平面的对称点也满足Γ的方程,

说明曲面Γ关于平面对称；同理,曲面Γ关于平面对称；关于平面对称.

由以上的讨论,可得曲面Γ的直观图如图所示.