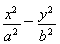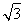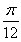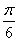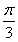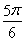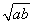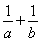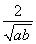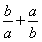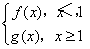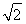题目内容
设定义在(0,+∞)上的函数f(x)=ax+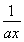 +b(a>0).
+b(a>0).
(1)求f(x)的最小值;
(2)若曲线y=f(x)在点(1,f(1))处的切线方程为y=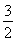 x,求a,b的值.
x,求a,b的值.
(1)b+2(2)a=2,b=-1
【解析】(1)f(x)=ax+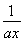 +b≥2
+b≥2 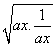 +b=b+2,
+b=b+2,
当且仅当ax=1 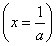 时,f(x)取得最小值为b+2.
时,f(x)取得最小值为b+2.
(2)由题意得:f(1)=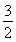 ?a+
?a+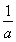 +b=
+b=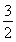 ,①
,①
f′(x)=a-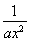 ⇒f′(1)=a-
⇒f′(1)=a-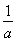 =
=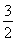 ,②
,②
由①②得:a=2,b=-1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目