Question

在平面直角坐标系中，已知焦距为4的椭圆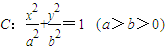的左、右顶点分别为A、B，椭圆C的右焦点为F，过F作一条垂直于x轴的直线与椭圆相交于R、S，若线段RS的长为．
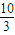（1）求椭圆C的方程；
（2）若椭圆C上存在两个不同的点关于直线l：y=9x+m对称，求实数m的取值范围．
（3）若P为椭圆C在第一象限的动点，过点P作圆x²+y²=5的两条切线PA、PB，切点为A、B，直线AB与x轴、y轴分别交于点M、N，求△MON（O为坐标原点）面积的最小值．

Answer 1

【答案】分析：（1）由题意得，c=2，故a²-b²=4，又椭圆过点（2，），代入椭圆方程，列方程求解a，b即可求椭圆C的方程；
（2）设D、E是椭圆C上关于l：y=9x+m对称的点，设直线DE的方程为；联立直线DE的方程与椭圆方程，根据判别式大于0求出n的范围；再结合D，E的中点在直线l上得到m和n的关系，即可求实数m的取值范围；
（3）设出P，A，B的坐标．得到直线PA与直线PB的方程，进而得到直线AB的方程，求出点M、N的坐标，表示出△MON的面积；再结合P为椭圆C在第一象限的动点即可求出面积的最小值．
解答：解：（1）依题意，椭圆过点，故，解得．…（3分）
椭圆C的方程为．…（4分）
（2）设D、E是椭圆C上关于l：y=9x+m对称的点，设直线DE的方程为．
联系方程得：，由△＞0得
又DE的中点在直线l上，代入得，
代入△得．
（3）设P（x，y），A（x₁，y₁），B（x₂，y₂）
则直线PA：x₁x+y₁y=5，直线PB：x₂x+y₂y=5
所以，直线AB：xx+yy=5，故，，所以，
而，当且仅当时等号成立．
此时．
点评：本题综合考查椭圆的性质及其应用、直线与椭圆的位置关系及直线，解题时要认真审题，注意运用方程思想等数学思想，同时考查了学生的基本运算能力、运算技巧、逻辑推理能力，难度较大．