题目内容
已知向量 ,
,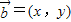 .
.(Ⅰ)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次,第二次出现的点数,求满足
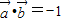 的概率;
的概率;(Ⅱ)若x,y∈[1,6],求满足
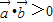 的概率.
的概率.
【答案】分析:(1)本小题考查的知识点是古典概型,关键是要找出满足条件满足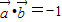 的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
(2)本小题考查的知识点是几何概型的意义,关键是要画出满足条件的图形,结合图形分析,找出满足条件的点集对应的图形面积,及图形的总面积.
解答: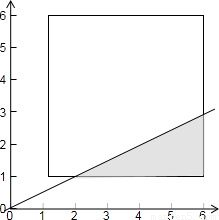 解:(Ⅰ)设(x,y)表示一个基本事件,
解:(Ⅰ)设(x,y)表示一个基本事件,
则抛掷两次骰子的所有基本事件有(1,1),(1,2),
(1,3),(1,4),(1,5),(1,6),(2,1),
(2,2),,(6,5),(6,6),共36个.(2分)
用A表示事件“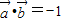 ”,即x-2y=-1
”,即x-2y=-1
则A包含的基本事件有(1,1),(3,2),(5,3),共3个.
∴P(A)=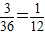
答:事件“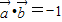 ”的概率为
”的概率为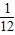
xyOOx=1Ox=6Oy=1Oy=6Ox-2y=0O
(Ⅱ)用B表示事件“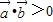 ”,即x-2y>0
”,即x-2y>0
试验的全部结果所构成的区域为
{(x,y)|1≤x≤6,1≤y≤6}
构成事件B的区域为
{(x,y)|1≤x≤6,1≤y≤6,x-2y>0}
如图所示:所以所求的概率为P(B)=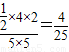
答:事件“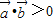 ”的概率为
”的概率为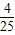
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.
几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=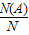 求解.
求解.
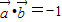 的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.(2)本小题考查的知识点是几何概型的意义,关键是要画出满足条件的图形,结合图形分析,找出满足条件的点集对应的图形面积,及图形的总面积.
解答:
 解:(Ⅰ)设(x,y)表示一个基本事件,
解:(Ⅰ)设(x,y)表示一个基本事件,则抛掷两次骰子的所有基本事件有(1,1),(1,2),
(1,3),(1,4),(1,5),(1,6),(2,1),
(2,2),,(6,5),(6,6),共36个.(2分)
用A表示事件“
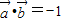 ”,即x-2y=-1
”,即x-2y=-1则A包含的基本事件有(1,1),(3,2),(5,3),共3个.
∴P(A)=
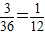
答:事件“
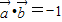 ”的概率为
”的概率为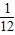
xyOOx=1Ox=6Oy=1Oy=6Ox-2y=0O
(Ⅱ)用B表示事件“
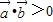 ”,即x-2y>0
”,即x-2y>0试验的全部结果所构成的区域为
{(x,y)|1≤x≤6,1≤y≤6}
构成事件B的区域为
{(x,y)|1≤x≤6,1≤y≤6,x-2y>0}
如图所示:所以所求的概率为P(B)=
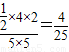
答:事件“
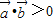 ”的概率为
”的概率为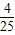
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.
几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
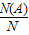 求解.
求解. 
练习册系列答案
相关题目
已知向量满足|
|=2|
|,若p:关于x的方程x2+|
|x+
•
=0没有实数根;q:向量
,
的夹角θ∈[0,
),则p是q的( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| π |
| 6 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
定义域为[a,b]的函数y=f(x)图象的两个端点为A、B,M(x,y)是f(x)图象上任意一点,其中x=λa+(1-λ)b∈[a,b],已知向量
=λ
+(1-λ)
,若不等式|
|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x-
在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
| ON |
| OA |
| OB |
| MN |
| 1 |
| x |
| A、[0,+∞) | ||||
B、[
| ||||
C、[
| ||||
D、[
|