题目内容
已知
（n∈N*）的展开式中含有常数项，则n的最小值是________．
7
分析：利用二项展开式的通项公式求出展开式的通项，令x的指数为0；得到n，r的关系，求出n的最小值．
解答：展开式的通项为Tr+1=2n-rCnrx2n-7r
令2n-7r=0即n=
（其中r=0，1，2，3..n）
∵n∈N*
所以当r=2时n最小为7
故答案为：7
点评：本题考查利用二项展开式的通项公式，解决二项展开式的特定项问题．
分析：利用二项展开式的通项公式求出展开式的通项，令x的指数为0；得到n，r的关系，求出n的最小值．
解答：展开式的通项为Tr+1=2n-rCnrx2n-7r
令2n-7r=0即n=
（其中r=0，1，2，3..n）∵n∈N*
所以当r=2时n最小为7
故答案为：7
点评：本题考查利用二项展开式的通项公式，解决二项展开式的特定项问题．
练习册系列答案
阅读快车系列答案
相关题目
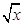)n的展开式中，某一项的系数是它前一项系数的2倍，而又等于它后一项系数的5/6.