Question

已知点A是抛物线y²=2px（p＞0）上一点，F为抛物线的焦点，准线l与x轴交与点K，已知|AK|=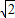|AF|，三角形AFK的面积等于8．
（Ⅰ）求p的值；
（Ⅱ）过该抛物线的焦点作两条互相垂直的直线l₁，l₂，与抛物线相交得两条弦，两条弦的中点分别为G，H．求|GH|的最小值．

Answer 1

【答案】分析：（Ⅰ）设A（x，y），因为抛物线的焦点F（，0），准线的方程为：x=-，K（-，0），作AM⊥l于M，则|AM|=x+=|AF|，由此能求出p．
（Ⅱ）由y²=8x，得F（2，0），设l₁的方程为y=k（x-2），l₂的方程为y=-（x-2）．由 得G（2+，），同理可得H（2+4k²，-4k），由此能求出|GH|的最小值．
解答：解：（Ⅰ）设A（x，y），
因为抛物线的焦点F（，0），
准线的方程为：x=-，K（-，0），
作AM⊥l于M，，
则|AM|=x+=|AF|
又|AK|=|AF|得|AK|=|AM|，
△AKM即为等腰直角三角形，
∴|KM|=|AM|=x+，即A（x，x+），
而A点在抛物线上，
∴=2px，
∴x=，于是（，p）．
又∵S_△AFK=•|KF|•|y|=•p•p==8，
p=4．
（Ⅱ）由y²=8x，得F（2，0），
显然直线l₁，l₂的斜率都存在且都不为0．
设l₁的方程为y=k（x-2），则l₂的方程为y=-（x-2）．
由 得G（2+，），
同理可得H（2+4k²，-4k）
则|GH|²=+
=16（k⁴++k²+）≥64．（当且仅当k²=时取等号）
所以|GH|的最小值是8．
点评：本题主要考查椭圆标准方程，简单几何性质，直线与抛物线的位置关系，抛物线的简单性质等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．