题目内容
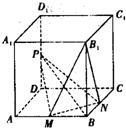 如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为棱AB、BC、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为棱AB、BC、DD1的中点.(1)求二面角B1-MN-B的正切值;
(2)证明:PB⊥平面B1MN;
(3)画出该正方体表面展开图,使其满足“有4个正方形连成一个长方形”的条件.
分析:(1)要求二面角B1-MN-B的正切值,我们要先找出二面角的平面角,再构造三角形,解三角形求出其正切值.
(2)要证明PB⊥平面B1MN,我们要在平面内找到两条与PB垂直的相交直线,分析题意可知B1M,B1N满足要求,进而可以转化为证明线线垂直.
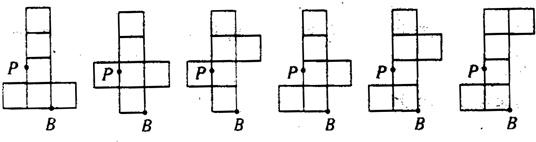
(3)由正方体12种展开图,选其中“1-4-1”的情况,再标识出P点即可.
(2)要证明PB⊥平面B1MN,我们要在平面内找到两条与PB垂直的相交直线,分析题意可知B1M,B1N满足要求,进而可以转化为证明线线垂直.
(3)由正方体12种展开图,选其中“1-4-1”的情况,再标识出P点即可.
解答:解:(1)连接BD交MN于F,则BF⊥MN,连接B1F.∵B1B⊥平面ABCD,
∴B1B⊥MN.
又∵BD⊥MN
∴MN⊥平面B1BF
∴MN⊥B1F
∴∠B1FB为二面角B1-MN-B的平面角.
在Rt△B1BF中,B1B=1,BF=
∴tan∠B1FB=2
(2)过点P作PE⊥AA1于E,
则PE⊥平面ABB1A1,
连接BE.由平面几何知识知,B1M⊥BE.
∴PB⊥B1M
同理,PB⊥B1N
又∵B1M∩B1N=B1
∴PB⊥平面B1MN.
(3)符合条件的正方体表面展开图可以是以下6种情况之一.
∴B1B⊥MN.
又∵BD⊥MN
∴MN⊥平面B1BF
∴MN⊥B1F
∴∠B1FB为二面角B1-MN-B的平面角.
在Rt△B1BF中,B1B=1,BF=
| ||
| 4 |
∴tan∠B1FB=2
| 2 |
(2)过点P作PE⊥AA1于E,
则PE⊥平面ABB1A1,
连接BE.由平面几何知识知,B1M⊥BE.
∴PB⊥B1M
同理,PB⊥B1N
又∵B1M∩B1N=B1
∴PB⊥平面B1MN.
(3)符合条件的正方体表面展开图可以是以下6种情况之一.

点评:线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.本题也可以用空间向量来解决,其步骤是:建立空间直角坐系?明确相关点的坐标?明确相关向量的坐标?通过空间向量的坐标运算求解.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )