题目内容

已知对所有实数x,不等式++<0恒成立,求a的取值范围.

      

思路分析:若令左式为y=,则y是x的二次函数,欲恒有y<0成立,那么其图象必开口向下,且全部图象在x轴下方与x轴无交点,即判别式Δ<0,从而求出a的取值范围.?

       解析:令y=［］x2+()x+,?要使各对数都有意义,必须满足条件:?

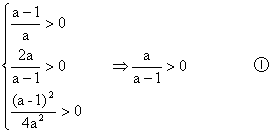
       抛物线开口向下,函数二次项系数应为负值,故必有<0,②?

       抛物线在x轴的下方且无交点则判别式?

       Δ=(2log2)2-4［］［］<0.③?

       由①知a>1或a<0;?

       由②有+log22<0,?

       即log2< ,?

       解得0<a<2.?

       联立①与②有1<a<2;再解③,先观察对数表达式中真数式的结构,?

       令z=,则可转化为关于z的二次不等式??

       (1+z)2-(1-z)·2(-1-z)<0,?

       整理得-(z+1)(z-3)<0.?

       解得z>3或z<-1,即有?

    >log28或<.?

       ∴a<或1>a>-1.?

       联立①②③得出a的取值范围为1<a<.?

       温馨提示:利用式子的变形、变换技巧将问题化简,是求解综合题常用的一种方法.巧妙的代换式是突破解题思路的关键,而综合运用知识则是获解的基本功.

练习册系列答案
相关题目
已知函数f（x）=x2-4x+a+3，g（x）=mx+5-2m．
（Ⅰ）若y=f（x）在[-1，1]上存在零点，求实数a的取值范围；
（Ⅱ）当a=0时，若对任意的x1∈[1，4]，总存在x2∈[1，4]，使f（x1）=g（x2）成立，求实数m的取值范围；
（Ⅲ）若函数y=f（x）（x∈[t，4]）的值域为区间D，是否存在常数t，使区间D的长度为7-2t？若存在，求出所有t的值；若不存在，请说明理由（注：区间[p，q]的长度为q-p）．
已知函数f（x）的定义域为R，对任意的x1，x2都满足f（x1+x2）=f（x1）+f（x2），
当x＜0时，f（x）＜0．
（1）判断f（x）的单调性；
（2）判断f（x）的奇偶性；
（3）是否存在这样的实数m，当θ∈[0，
π2
]时，使不等式f[cos2θ-（2+m）sinθ]+f（3+2m）＞0对所有θ恒成立，若存在，求出m的取值范围；若不存在，说明理由．
给出下列命题：
（1）已知可导函数f（x），x∈D，则函数f（x）在点x0处取得极值的充分不必要条件是f′（x0）=0，x0∈D．
（2）已知命题P：?x∈R，sinx≤1，则￢p：?x∈R，sinx＞1．
（3）已知命题p：
1
x 2-3x+2
＞0，则￢p：
1
x 2-3x+2
≤0．
（4）给定两个命题P：对任意实数x都有ax2+ax+1＞0恒成立；Q：关于x的方程x2-x+a=0有实数根．如果P∧Q为假命题，P∨Q为真命题，则实数a的取值范围是(-∞，0)∪(
1
4
，4)．
其中所有真命题的编号是
（2），（4）
（2），（4）
．
已知函数f（x）=x3-
3
4
(a+4)x2+
3
2
(a+2)x，a∈R．
（Ⅰ）当a=2时，求f（x）的单调区间；
（Ⅱ）是否存在实数a∈（0，2]，使得对任意的x∈[0，a]，不等式0≤f（x）≤a恒成立？若存在，求出所有a的值；若不存在，请说明理由．
有如下四个命题：①命题“有的三角形是直角三角形”的否定为“所有的三角形都不是直角三角形”；②不等式|x-2010|+|x-2011|＜a在R上有解，则实数a的取值范围是（1，+∞）；③已知函数f（x）=sin（2x+θ）（θ∈R），且对?x∈R，f(
π2
-x)=-f(x)，则cos（2θ）=-1；④若偶函数f（x）=loga|x+b|（a＞0，a≠1）在（-∞，0）内单调递增，则f（a+1）＜f（b+2）其中真命题的序号为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网