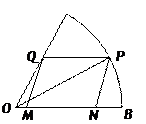题目内容
如图,从圆 外一点
外一点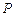 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为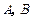 ,
,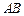 与
与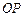 交于点
交于点 ,设
,设 为过点
为过点 且不过圆心
且不过圆心 的一条弦,求证:
的一条弦,求证: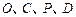 四点共圆.
四点共圆.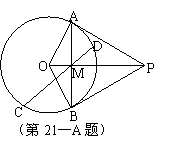
因为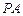 ,
,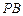 为圆
为圆 的两条切线,所以
的两条切线,所以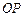 垂直平分弦
垂直平分弦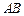 ,
,
在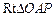 中,
中,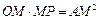 ,
,
在圆 中,
中, ,
,
所以,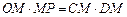 ,
,
又弦 不过圆心
不过圆心 ,所以
,所以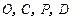 四点共圆.
四点共圆.
解析

练习册系列答案
相关题目
曲线的参数方程为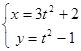 (t是参数),则曲线是( )
(t是参数),则曲线是( )
| A.线段 | B.直线 | C.圆 | D.射线 |
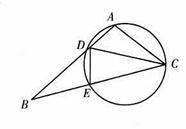
 是圆内接四边形,延长
是圆内接四边形,延长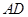 与的延长线
与的延长线 交于点
交于点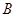 ,且
,且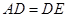 ,
, 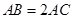 .
.
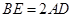 ;
;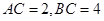 时,求
时,求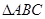 的外接圆的切线
的外接圆的切线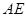 与
与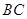 的延长线交于点
的延长线交于点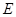 ,
,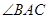 的平分线与
的平分线与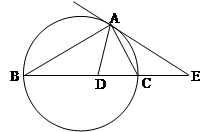
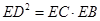
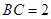 ,
, =1.求
=1.求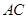 长.
长.
 经过
经过 ⊙O上一点
⊙O上一点 ,且
,且 ,
,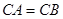 ,⊙O交直线
,⊙O交直线 于
于 .
.
 ⊙O的半径为3,求
⊙O的半径为3,求 的长.
的长. 中,
中, ,
,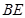 平分
平分 交
交 于点
于点 ,点
,点 在
在 上,
上, .
.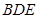 的外接圆的切线;
的外接圆的切线;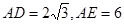 ,求
,求 的长.
的长.
 •BD
•BD