题目内容
设y1=a3x+1,y2=a-2x(a>0,a≠1),确定x为何值时,有:(1)y1=y2 ;
(2)y1>y2.
【答案】分析:先将两个函数抽象为指数函数:y=ax,则
(1)转化为关于x的方程:3x-1=-2x求解.
(2)0<a<1,y=ax是减函数,有3x-1<-2x求解,当a>1时,y=ax是增函数,有3x-1>-2x求解,然后两种情况取并集.
解答:解:(1)因为y1=y2
∴3x+1=-2x
解之得: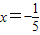
(2)因为a>1,所以指数函数为增函数.
又因为y1>y2,所以有3x-1>-2x
解得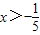 ;
;
若0<a<1,指数函数为减函数.
因为y1>y2,
所以有3x-1<-2x
解得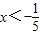
综上: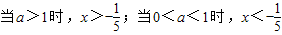 .
.
点评:本题主要考查指数不等式的解法,这类问题要转化为指数函数的单调性来解.
(1)转化为关于x的方程:3x-1=-2x求解.
(2)0<a<1,y=ax是减函数,有3x-1<-2x求解,当a>1时,y=ax是增函数,有3x-1>-2x求解,然后两种情况取并集.
解答:解:(1)因为y1=y2
∴3x+1=-2x
解之得:
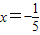
(2)因为a>1,所以指数函数为增函数.
又因为y1>y2,所以有3x-1>-2x
解得
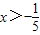 ;
;若0<a<1,指数函数为减函数.
因为y1>y2,
所以有3x-1<-2x
解得
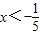
综上:
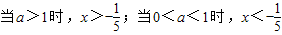 .
.点评:本题主要考查指数不等式的解法,这类问题要转化为指数函数的单调性来解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目