题目内容
在△ABC中,已知tanA,tanB是方程x2+
x-2=0的两根,则∠C为( )
| 3 |
分析:先由韦达定理求出tanA+tanB,tanA×tanB,再由两角和的正切公式即可计算出tanC值,即可得出角C的大小.
解答:解:∵方程x2+
x-2=0的判别式△>0,
∴tanA+tanB=-
tanA×tanB=-2
∴tanC=tan[π-(A+B)]=-tan(A+B)=-
=-
=
∵0<C<π
∴C=
故选:B.
| 3 |
∴tanA+tanB=-
| 3 |
∴tanC=tan[π-(A+B)]=-tan(A+B)=-
| tanA+tanB |
| 1-tanA•tanB |
-
| ||
| 1+2 |
| ||
| 3 |
∵0<C<π
∴C=
| π |
| 6 |
故选:B.
点评:本题综合考查了一元二次方程根与系数的关系,两角和的正切公式,解题时要牢记公式,认真计算

练习册系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.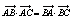 .
. |=|
|=| |;
|; ,求|
,求| -t
-t