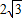Question

设P为直线3x+4y+3=0上的动点，过点P作圆C：x²+y²-2x-2y+1=0的两条切线，切点分别为A，B，则四边形PACB的面积的最小值为（　　）

• A、1
• B、

  3

  2

• C、2

  3

• D、

  3

Answer 1

分析：由圆的方程为求得圆心C（1，1）、半径r为：1，由“若四边形面积最小，则圆心与点P的距离最小时，即距离为圆心到直线的距离时，切线长PA，PB最小”，最后将四边形转化为两个直角三角形面积求解．

解答：解：∵圆的方程为：x²+y²-2x-2y+1=0
∴圆心C（1，1）、半径r为：1
根据题意，若四边形面积最小
当圆心与点P的距离最小时，距离为圆心到直线的距离时，
切线长PA，PB最小
圆心到直线的距离为d=2
∴|PA|=|PB|=

d2-r2

=

3

∴sPACB=2|PA|r=

3

故选D．

点评：本题主要考查直线与圆的位置关系，主要涉及了构造四边形及其面积的求法，同时，还考查了转化思想．此题属中档题．