题目内容
(本小题共13分)
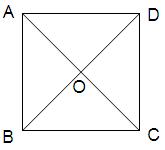
已知正方形ABCD的边长为1,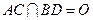 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线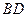 折起,使
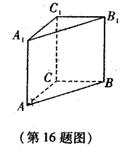
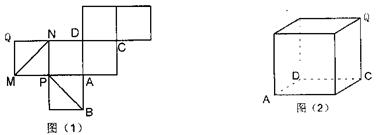
折起,使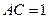 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.
(I)若点M是棱AB的中点,求证:OM∥平面ACD;
(II)求证: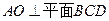 ;
;
(III)求二面角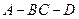 的余弦值.
的余弦值.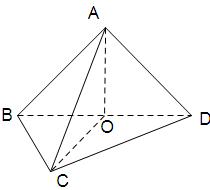
已知正方形ABCD的边长为1,
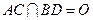 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线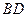 折起,使
折起,使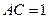 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.(I)若点M是棱AB的中点,求证:OM∥平面ACD;
(II)求证:
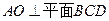 ;
;(III)求二面角
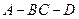 的余弦值.
的余弦值.


(1)略
(2)略
(3)
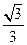
解:(I)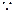 在正方形ABCD中,
在正方形ABCD中,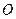 是对角线
是对角线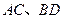 的交点,
的交点,
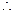 O为BD的中点, ---------------------1分
O为BD的中点, ---------------------1分
又M为AB的中点,
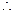 OM∥AD. ---------------------2分
OM∥AD. ---------------------2分
又AD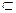 平面ACD,OM
平面ACD,OM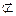 平面ACD, ---------------------3分
平面ACD, ---------------------3分
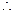 OM∥平面ACD. ---------------------4分
OM∥平面ACD. ---------------------4分
(II)证明:在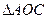 中,
中,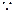
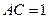 ,
,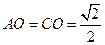 , ---------------------5分
, ---------------------5分
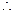
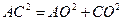 ,
,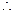
 . ---------------------6分
. ---------------------6分
又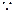
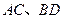 是正方形ABCD的对角线,
是正方形ABCD的对角线,
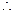
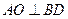 , --------------------7分
, --------------------7分
又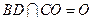
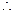
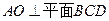 . --------------------8分
. --------------------8分
(III)由(II)知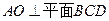 ,则OC,OA,OD两两互相垂直,如图,以O为原点,建立
,则OC,OA,OD两两互相垂直,如图,以O为原点,建立
空间直角坐标系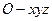 .
.
则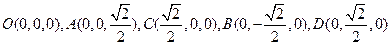 ,
,
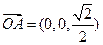 是平面
是平面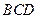 的一个法向量. --------------------9分
的一个法向量. --------------------9分
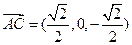 ,
,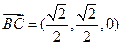 ,
,
设平面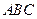 的法向量
的法向量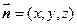 ,则
,则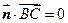 ,
,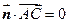 .
.
即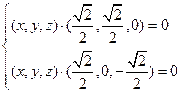 , --------------------11分
, --------------------11分
所以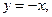 且
且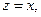 令
令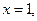 则
则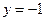 ,
,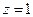 ,解得
,解得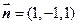 .
.
--------------------12分
从而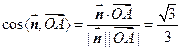 ,二面角
,二面角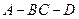 的余弦值为
的余弦值为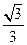 ..
..
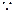 在正方形ABCD中,
在正方形ABCD中,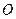 是对角线
是对角线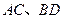 的交点,
的交点,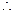 O为BD的中点, ---------------------1分
O为BD的中点, ---------------------1分又M为AB的中点,
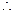 OM∥AD. ---------------------2分
OM∥AD. ---------------------2分又AD
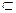 平面ACD,OM
平面ACD,OM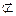 平面ACD, ---------------------3分
平面ACD, ---------------------3分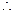 OM∥平面ACD. ---------------------4分
OM∥平面ACD. ---------------------4分(II)证明:在
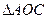 中,
中,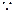
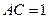 ,
,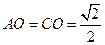 , ---------------------5分
, ---------------------5分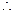
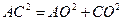 ,
,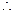
 . ---------------------6分
. ---------------------6分又
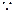
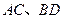 是正方形ABCD的对角线,
是正方形ABCD的对角线,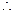
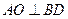 , --------------------7分
, --------------------7分又
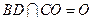
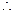
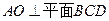 . --------------------8分
. --------------------8分(III)由(II)知
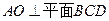 ,则OC,OA,OD两两互相垂直,如图,以O为原点,建立
,则OC,OA,OD两两互相垂直,如图,以O为原点,建立空间直角坐标系
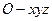 .
.则
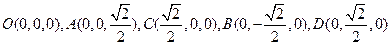 ,
, 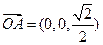 是平面
是平面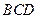 的一个法向量. --------------------9分
的一个法向量. --------------------9分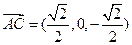 ,
,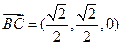 ,
, 设平面
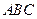 的法向量
的法向量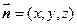 ,则
,则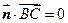 ,
,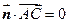 .
.即
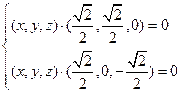 , --------------------11分
, --------------------11分所以
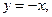 且
且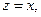 令
令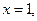 则
则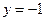 ,
,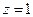 ,解得
,解得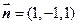 .
. --------------------12分
从而
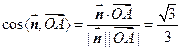 ,二面角
,二面角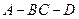 的余弦值为
的余弦值为 ..
..
练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
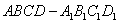 中,
中,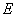 、
、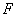 分别是棱
分别是棱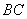 ,
,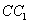 上的点,
上的点,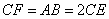 ,
,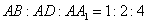 .
.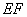 与
与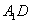 所成角的余弦值;
所成角的余弦值;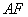
 平面
平面
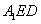 ;
;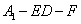 的正弦值.
的正弦值.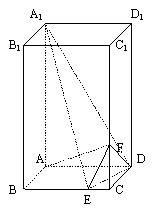
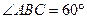 ,
,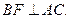

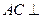 面ABF;
面ABF;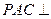 平面BCEF?若存在,求出
平面BCEF?若存在,求出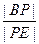 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。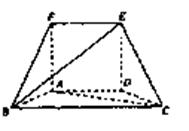

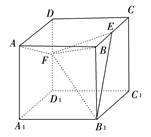
 中,
中, ,
, .
.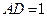 ,
,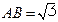 ,
,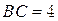 .
.
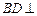
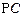 ;
;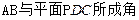 ;
;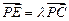 ,若
,若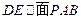 ,求
,求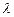 的值。
的值。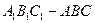 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面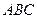 为等腰直角三角形,
为等腰直角三角形, 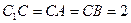 ,点
,点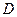 为棱
为棱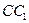 的中点,点
的中点,点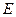 在棱
在棱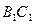 上运动.
上运动.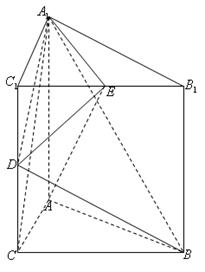
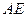 ;
;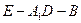 的平面角的余弦值为
的平面角的余弦值为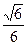 ,求点
,求点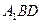 的距离;
的距离;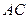 上是否存在一点
上是否存在一点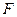 ,使得
,使得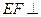 平面
平面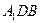 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.