题目内容
已知函数f(x)=x2(x-t),t>0.(I)求函数f(x)的单调区间;
(II)设函数y=f(x)在点P(x,y)处的切线的斜率为k,当x∈(0,1]时,
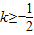 恒成立,求t的最大值.
恒成立,求t的最大值.
【答案】分析:(I)求导函数,根据导数的正负可得函数的单调区间;
(II)当x∈(0,1]时,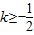 恒成立,等价于x∈(0,1]时,
恒成立,等价于x∈(0,1]时,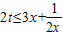 恒成立,求出右边函数的最值,即可求得结论.
恒成立,求出右边函数的最值,即可求得结论.
解答:解:(I)求导函数可得f′(x)=x(3x-2t)
令f′(x)>0,∵t>0,∴x<0或x>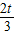 ;
;
令f′(x)<0,∵t>0,∴0<x<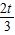 ;
;
∴函数的单调增区间为(-∞,0),(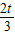 ,+∞);单调减区间为(0,
,+∞);单调减区间为(0,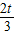 );
);
(II)∵当x∈(0,1]时,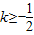 恒成立,
恒成立,
∴x∈(0,1]时,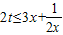 恒成立
恒成立
∵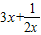 ≥
≥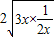 =
=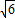 (当且仅当x=
(当且仅当x=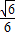 时取等号)
时取等号)
∴2t≤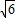 ,∴t≤
,∴t≤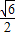 ,
,
∴t的最大值为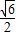 .
.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生的计算能力,属于中档题.
(II)当x∈(0,1]时,
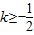 恒成立,等价于x∈(0,1]时,
恒成立,等价于x∈(0,1]时,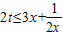 恒成立,求出右边函数的最值,即可求得结论.
恒成立,求出右边函数的最值,即可求得结论.解答:解:(I)求导函数可得f′(x)=x(3x-2t)
令f′(x)>0,∵t>0,∴x<0或x>
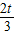 ;
;令f′(x)<0,∵t>0,∴0<x<
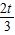 ;
;∴函数的单调增区间为(-∞,0),(
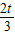 ,+∞);单调减区间为(0,
,+∞);单调减区间为(0,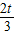 );
);(II)∵当x∈(0,1]时,
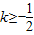 恒成立,
恒成立,∴x∈(0,1]时,
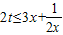 恒成立
恒成立∵
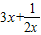 ≥
≥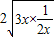 =
=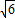 (当且仅当x=
(当且仅当x=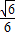 时取等号)
时取等号)∴2t≤
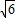 ,∴t≤
,∴t≤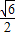 ,
,∴t的最大值为
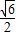 .
.点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|