题目内容
已知圆![]() :
:![]() 及定点
及定点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且满足
上,且满足![]() =2
=2![]() ,
,![]() ·
·![]() =
=![]() .
.
(1)若![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若动圆![]() 和(1)中所求轨迹
和(1)中所求轨迹![]() 相交于不同两点
相交于不同两点![]() ,
,![]() 是否存在一组正实数
是否存在一组正实数![]() ,使得直线
,使得直线![]() 垂直平分线段
垂直平分线段![]() ,若存在,求出这组正实数;若不存在,说明理由.
,若存在,求出这组正实数;若不存在,说明理由.
解:(1)![]()
∴点![]() 为
为![]() 的中点,
的中点,
又![]() ,
,
![]() 或
或![]() 点与
点与![]() 点重合.
点重合.
∴![]() ………
………![]() …2分
…2分
又![]()
∴点![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,
为焦点的椭圆,
且![]() ,
,
∴![]()
∴G的轨迹方程是![]() …………6分
…………6分
(2)解:不存在![]() 这样一组正实数,
这样一组正实数,
下面证明: …………7分
由题意,若存在这样的一组正实数,
当直线![]() 的斜率存在时,设之为
的斜率存在时,设之为![]() ,
,
故直线![]() 的方程为:
的方程为:![]() ,设
,设![]() ,
,![]() 中点
中点![]() ,
,
则 ,两式相减得:
,两式相减得:
![]() .…………9分
.…………9分
注意到![]() ,
,
且 ,
,
则![]() , ②
, ②
又点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
代入②式得:![]() .
.
因为弦![]() 的中点
的中点![]() 在⑴所给椭圆
在⑴所给椭圆![]() 内,
内,
故![]() ,
,
这与![]() 矛盾,
矛盾,
所以所求这组正实数不存在. …………13分
当直线![]() 的斜率不存在时,
的斜率不存在时,
直线![]() 的方程为
的方程为![]() ,
,
则此时![]() ,
,
代入①式得![]() ,
,
这与![]() 是不同两点矛盾.综上,所求的这组正实数不存在. …………14分
是不同两点矛盾.综上,所求的这组正实数不存在. …………14分

练习册系列答案
相关题目
 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足 :
: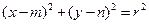 及定点
及定点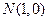 ,点
,点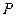 是圆
是圆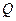 在
在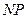 上,点
上,点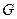 在
在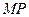 上,
上,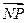 =2
=2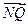 ,
,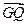 ·
·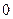 .
.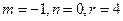 ,求点
,求点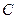 的方程;
的方程;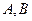 ,是否存在一组正实数
,是否存在一组正实数 ,使得直线
,使得直线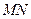 垂直平分线段
垂直平分线段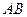 ,若存在,求出这组正实数;若不存在,说明理由.
,若存在,求出这组正实数;若不存在,说明理由.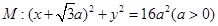 及定点
及定点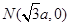 ,点
,点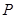 是圆
是圆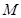 上的动点,点
上的动点,点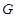 在
在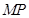 上,且满足
上,且满足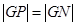 ,
,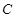 。
。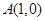 关于直线
关于直线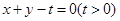 的对称点在曲线
的对称点在曲线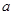 的取值范围。
的取值范围。