题目内容
已知数列{an}中,a2=1,前n项和为Sn,且 .
.
(1)求a1,a3;
(2)求证:数列{an}为等差数列,并写出其通项公式;
(3)设 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
解:(1)令n=1,则a1=S1=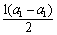 =0. a3=2;
=0. a3=2;
(2)由 ,即
,即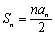 ,①得
,①得 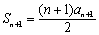 . ②
. ②
②-①,得 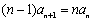 .③
.③
于是, .④
.④
③+④,得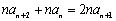 ,即
,即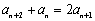 .
.
又a1=0,a2=1,a2-a1=1,
所以,数列{an}是以0为首项,1为公差的等差数列.所以,an=n-1.
(3)假设存在正整数数组(p,q),使b1,bp,bq成等比数列,
则lgb1,lgbp,lgbq成等差数列, 于是,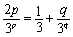 .
.
所以, (☆).易知(p,q)=(2,3)为方程(☆)的一组解.
(☆).易知(p,q)=(2,3)为方程(☆)的一组解.
当p≥3,且p∈N*时,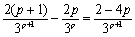 <0,
<0,
故数列{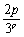 }(p≥3)为递减数列 于是
}(p≥3)为递减数列 于是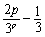 ≤
≤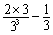 <0,所以此时方程(☆)无正整数解.
<0,所以此时方程(☆)无正整数解.
综上,存在唯一正整数数对(p,q)=(2,3),使b1,bp,bq成等比数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则
,则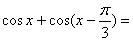 ( )
( )
 B.
B.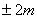 C.
C.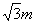 D.
D.
 的方程为
的方程为 ,右焦点为
,右焦点为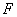 ,直线
,直线 与圆
与圆 相切于点
相切于点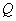 ,且
,且 轴的右侧,设直线
轴的右侧,设直线 .
. ,求直线
,求直线
 .
.
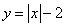 的图像与曲线
的图像与曲线 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数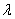
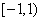 B.
B. 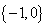 C.
C.  D.
D. 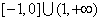
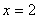 与双曲线
与双曲线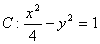 的渐近线交于
的渐近线交于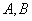 两点,设
两点,设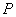 为双曲线
为双曲线 上的任意一点,若
上的任意一点,若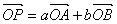 (
(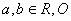 为坐标原点),则下列不等式恒成立的是( )
为坐标原点),则下列不等式恒成立的是( )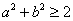 B.
B.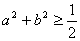
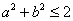 D.
D.
 .
. (
( 为常数,
为常数, ),且
),且 是方程
是方程 的解.当
的解.当
 值域为 .
值域为 . ,元素
,元素
 的代数余子式为
的代数余子式为 ,
, , 函数
, 函数 的定义域为
的定义域为 若
若 求实数
求实数 的取值范围.
的取值范围.
 ,侧面积为
,侧面积为
 ,则此圆锥的体积为________
,则此圆锥的体积为________ .
.