Question

在五棱锥P-ABCDE中，PA=AB=AE=2a，PB=PE=a，BC=DE=a，∠EAB=∠ABC=

∠DEA=90°．

（1）求证：PA⊥平面ABCDE；（2）若为中点，求证：平面

（3）求二面角A-PD-E的正弦值；（4）求点C到平面PDE的距离

                            

Answer 1

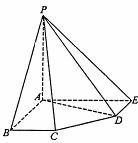
解：（1）证明∵PA=AB=2a，PB=2a,∴PA²+AB²=PB²，∴∠PAB=90°，

即PA⊥AB．同理PA⊥AE． ∵AB∩AE=A，∴PA⊥平面ABCDE． 

（2）∵∠AED＝90°，∴AE⊥ED．∵PA⊥平面ABCDE，∴PA⊥ED．∴ED⊥平面PAE，所以DE⊥AG。，为中点，所以AG⊥PE，

∴AG⊥平面PDE                             

（3）∵∠AED＝90°，∴AE⊥ED．∵PA⊥平面ABCDE，∴PA⊥ED．∴ED⊥平面PAE．过A作AG⊥PE于G，过DE⊥AG，                      

∴AG⊥平面PDE．过G作GH⊥PD于H，连AH，由三垂线定理得AH⊥PD．

∴∠AHG为二面角A-PD-E的平面角．                                               

在直角△PAE中，AG＝a．在直角△PAD中，AH＝a，∴在直角△AHG中，

sin∠AHG＝＝．∴二面角A-PD-E的正弦值为．         

（4）∵∠EAB=∠ABC=∠DEA=90°,  BC=DE=a, AB=AE=2a, 取AE中点F，连CF，

∵AF∥=BC,∴四边形ABCF为平行四边形．∴CF∥AB，而AB∥DE，∴CF∥DE，

而DE平面PDE，CF平面PDE，∴CF∥平面PDE．

∴点C到平面PDE的距离等于F到平面PDE的距离．

∵PA⊥平面ABCDE，∴PA⊥DE．又∵DE⊥AE，∴DE⊥平面PAE．

∴平面PAE⊥平面PDE．∴过F作FG⊥PE于G，则FG⊥平面PDE．

∴FG的长即F点到平面PDE的距离．      

在△PAE中，PA=AE=2a，F为AE中点，FG⊥PE，   ∴FG=a．

∴点C到平面PDE的距离为a．（或用等体积法求）